Квазилинейное уравнение

Сильные и слабые разрывы. При решении линейного уравнения переноса разрывы в решениях появляются в связи с разрывами либо в начальных, либо в граничных условиях. В квазилинейных уравнениях, даже при наличии гладкости в начальных и граничных условиях, решения могут стать разрывными. Исследуем вопрос об образовании разрывов на примере решения простейшего квазилинейного уравнения

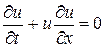, (28)

которое возникает при одномерном описании движения жидкости и газа. В уравнении переноса (28) скорость переноса определяется самим решением, т.е. c = u(t,x).

В дальнейшем будем рассматривать простейший случай уравнения (28), когда решение u знакопостоянно u(t,x) > 0 и граничное и начальное значения на положительных полуосях системы координат (t,x) полностью определяют решение в первом квадранте. Поскольку граничное и начальное значения передаются по характеристикам x - ut = const, а их наклон зависит от решения, постольку возможны такие начальные данные, при которых характеристики могут пересекаться, что приводит к появлению разрывных решений. С этой точки зрения существует четыре типа начальных данных.

Первый тип начальных данных. Начальные и граничные являются непрерывными функциями такими, что u(0,x) монотонно не убывает, а u(t,0) монотонно не возрастает и они непрерывно согласованы в начале координат.

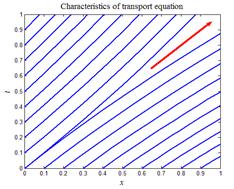
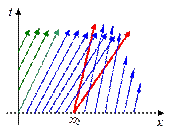
Наклон (тангенс угла наклона к оси x) характеристик в каждой точке плоскости (t,x) равен 1/u(t,x). При данном типе начальных данных наклон монотонно и непрерывно убывает слева направо (рис.11,а). Первый квадрант всюду плотно покрыт характеристиками и через каждую точку проходит одна и только одна характеристика. По этим характеристикам в данную точку переносится либо граничное, либо начальное значения. Решение однозначно определено и непрерывно во всем квадранте.

Для примера возьмем следующие граничные и начальные условия

,

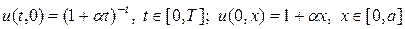тогда характеристики, выходящие из точек (t,0), t Î [0,T] и (0,x), x Î [0,a], в окрестности этих точек удовлетворяют уравнениям:

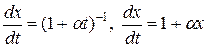. (29)

Решая уравнения (29), можно найти два класса приближенных характеристик, выходящих из граничного и начального условий, т.е.

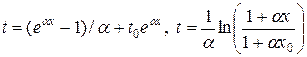, (30)

где t₀, x₀ — константы, пробегающие значения по отрезку [0,T] и отрезку [0,a] соответственно.

На листинге_№8 приведен код небольшой программы, которая изображает приближенные характеристики (30) в области G = [0,T]´[0,a]. Итог работы кода программы листинга_№8 приведен на рис.11,а. Стрелка на рис.11,а указывает общее направление переноса граничных и начальных условий.

Листинг_№8

%Программа рисования приближенных

%характеристик (30)

%очищаем рабочее пространство

clear all

%задаем размеры области G=[0,T]x[0,a] и

%константу alpha

T=1; a=1; alpha=0.3;

%определяем набор значений констант t0 и x0

t0=0:0.1:T; x0=0:0.1:a;

t=0:0.1:T; x=0:0.1:a;

%рисуем характеристики, выходящие из

%левого граничного условия

for m=1:length(t0)

for n=1:length(x)

y(n)=(exp(alpha*x(n))-1)/alpha+...

t0(m)*exp(alpha*x(n));

end

plot(x,y);

hold on

end

%рисуем характеристики, выходящие из

%начального условия

for n=1:(length(x0)-1)

x=x0(n):((a-x0(n))/10):a;

for nn=1:length(x)

y(nn)=log((1+alpha*x(nn))/...

(1+alpha*x0(n)))/alpha;

end

plot(x,y);

hold on

end

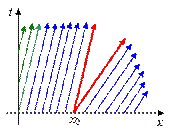
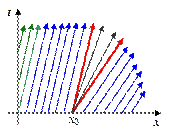
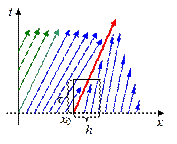
Рис.11,а. Характеристики первого типа начальных данных	Рис.11,б. Характеристики второго типа начальных данных с пустой областью	Рис.11,в. Характеристики второго типа начальных данных с доопределенной пустой областью

Второй тип начальных данных. Краевое и начальное значения монотонны как в первом случае, но имеют разрывы. Для упрощения ситуации положим

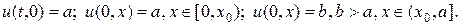(31)

На рис.11,б приведены соответствующие характеристики. В силу (31) характеристики приближенно можно представить прямыми линиями, которые имеют одинаковый наклон левее и правее точки разрыва x₀. Из точки разрыва начальных данных x₀ выходит две характеристики, выделенные на рис.11,б жирными стрелками красного цвета. Между этими линиями нет ни одной характеристики и решение в этой области не определено.

Потребуем, чтобы задача была корректной, т.е. устойчивой относительно бесконечно малых возмущений начальных данных. Для этого заменим разрыв в начальных данных на монотонный переход в бесконечно узком интервале. Тогда пустая область на рис.11,б будет заполнена набором характеристик, аналитический вид которых следующий:

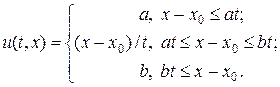(32)

На рис.11,в приведен вид характеристик (две черные стрелки) в пустой области разрыва начальных данных. В итоге доопределения с помощью (32) решение непрерывно на всей плоскости, кроме точки (0,x₀). Таким образом, разрыв начальных данных сглаживается со временем, но след разрыва остается. Этот след в виде разрыва производных передается по двум характеристикам, выходящим из точки разрыва x₀. Во всех остальных точках решение будет гладким, если соответствующие граничные и начальные данные были гладкими.

Разрыв производных называют слабым разрывом решения. Слабые разрывы квазилинейного уравнения переносятся по характеристикам.

Третий тип начальных данных. Пусть нарушено условие монотонности, предполагаемое в двух предыдущих случаях. Положим, как и в (31),

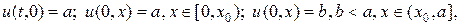
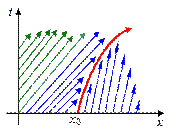
но теперь a > b > 0. В этом случае характеристики будут иметь вид, представленный на рис.12,а.

В угле, образованном жирными (красными) стрелками, через каждую точку проходит две характеристики, каждая из которых приносит свое значение начальных данных, т.е. вне этого угла решение однозначно определено, а внутри угла решение однозначно не определено. В этом случае непрерывное решение построить не удается, т.е. решение должно быть разрывным или обобщенным решением дифференциального уравнения (28).

Обобщенное решение удовлетворяет некоторому интегральному уравнению, которое получается из специальной дивергентной формы записи дифференциального уравнения. Разные дивергентные формы записи одного и того же уравнения приводят к разным разрывным решениям, при этом гладкие решения для всех дивергентных форм одинаковы. Дивергентная форма, представляющая физический закон сохранения, определяет правильное решение, которое еще называют допустимым.

Рис.12,а. Характеристики третьего типа начальных данных	Рис.12,б. Построение обобщенного, разрывного решения	Рис.12,в. Обобщенное, разрывное решение и поле характеристик

Квазилинейное уравнение переноса (28) легко переписать в одной из дивергентных форм:

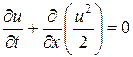. (33)

Нас интересует решение, имеющее единственный разрыв. Пусть наклон линии разрыва соответствует скорости V, и разрыв двигается как волна. Из вида характеристик на рис.12,а следует, что искомое разрывное решение должно иметь следующий вид:

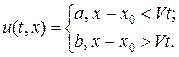
Проинтегрируем дивергентную форму (33) по площади прямоугольника со сторонами t и h = Vt, и левый нижний угол которого находится в точке разрыва x₀ (рис.12,б), тогда

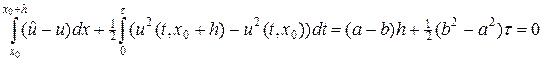
откуда находим скорость распространения разрыва

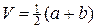. (34)

Разрыв решения называют сильным разрывом, а в газовой динамике такой разрыв называют ударной волной. Сильный разрыв квазилинейного уравнения переноса распространяется не по характеристике. Так, на рис.12,б жирная стрелка, по которой распространяется разрыв, не является характеристикой. В теории квазилинейных уравнений доказывается, что только обобщенное решение устойчиво относительно малых возмущений начальных данных.

Четвертый тип начальных данных. В этом случае функция начального условия u(0,x) непрерывна и убывает на некотором интервале, что переадресует нас к третьему типу. Пересечение характеристик также приводит к образованию сильного разрыва (рис.12,в), скорость которого описывается уравнением, подобным (34). Однако в этом случае скорость сильного разрыва может меняться.

Псевдовязкость. Основную трудность при расчетах по разностным схемам доставляют сильные разрывы решения. Прием по преодолению этой трудности состоит в том, чтобы внести в исходное уравнение такую “малую” добавку, чтобы исходные разрывные решения стали непрерывными и достаточно гладкими. Составляя для нового уравнения соответствующую разностную схему, можно получить нужное решение.

Гладкие решения характерны для уравнений с диссипативными членами типа диффузии, теплопроводности или вязкого трения. Добавляемый в исходное уравнение член, оказывающий выглаживающее воздействие, принято называть псевдовязкостью или искусственной, математической вязкостью.

Рассмотрим пример. Добавим в исходное квазилинейное уравнение (28) соответствующий член, тогда

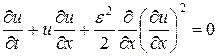, (35)

где третье слагаемое выступает в качестве псевдовязкости, а коэффициент e ² считается малым.

Видно, что для гладких, дважды непрерывно-дифференцируемых функций решения уравнения (28) близки к решениям уравнения (35).

Поищем среди гладких решений уравнения (35) решение, напоминающее ударную волну:

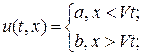
где b < a и скорость ударной волны 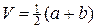. Рассмотрим автомодельное решение в виде бегущей волны

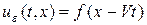. (36)

После подстановки (36) в (35), находим

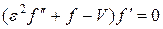. (37)

Приравнивая каждый из сомножителей в (37) к нулю, получаем два решения:

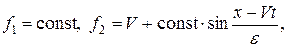
из которых можно сконструировать решение, похожее на слегка размытую с шириной ~e ударную волну:

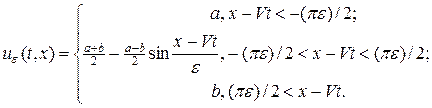(38)

Решение (38) непрерывно-дифференцируемо и при e ® 0 сходится к разрывному решению — ударной волне. На листинге_№9 приведен код программы рисования последовательности профилей (38), приводящих к образованию ударной волны при e ® 0. Итоговый рисунок приведен на рис.13.

Листинг_№9

%Программа рисования по формуле (38)

%последовательности формирования

%ударной волны при eps -> 0

%очищаем рабочее пространство

clear all

%задаем параметры функции (38)

a=2; b=0.2; eps=2;

%определяем переменную xi=x-Vt

xi=-2:0.01:2;

%Формируем цикл построения графиков

%ueps при различных значениях eps

for i=1:10

%уменьшаем текущее значение

%значение eps вдвое

eps=eps/2;

for j=1:length(xi)

if xi(j)<-0.5*pi*eps

ueps(j)=a;

end

if (xi(j)>=(-0.5*pi*eps))&...

(xi(j)<=(0.5*pi*eps))

ueps(j)=0.5*(a+b)-...

0.5*(a-b)*sin(xi(j)/eps);

end

if xi(j)>0.5*pi*eps

ueps(j)=b;

end

end

axis([-2 2 0 2]);

plot(xi,ueps,'LineWidth',2);

hold on

end

Обычно коэффициент псевдовязкости связывается с шагом сетки по пространству, т.е. считают, что

e = n h, n = const, (39)

тогда любой сильный разрыв согласно (38) размазывается на одно и то же число шагов сетки pe / h = pn. В этом случае при h ® 0 уравнение с псевдовязкостью переходит в исходное квазилинейное уравнение (28), а размазанная ударная волна (38) переходит в разрывную ударную волну.

Составим для уравнения с псевдовязкостью (35) явную разностную схему на равномерной сетке:

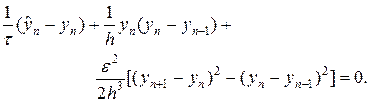(40)

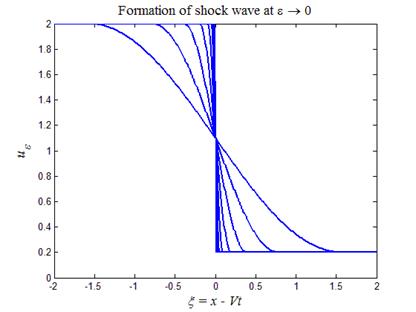
Рис.13. Образование разрывного решения — ударной
волны при e ® 0 согласно представлению (38)

Исследуем вопрос об устойчивости разностной схемы (40). Поскольку разностная схема (40) является нелинейной, линеаризуем ее, определяя уравнение для погрешности dy:

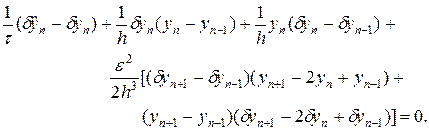(41)

Поскольку коэффициенты при dy являются переменными, для дальнейшего исследования вопроса устойчивости схемы (40) воспользуемся принципом “замороженных” коэффициентов. Согласно этому принципу коэффициенты при dy считаются постоянными величинами. Проведем в (41) замены 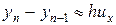и т.д., тогда

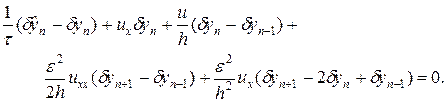(42)

Изучим рост ошибки, которая имеет вид 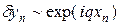. Подставим в (42) выражения

,

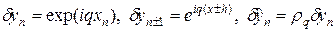тогда множитель роста гармоники 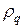предстанет в виде:

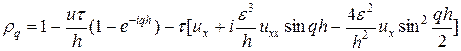. (43)

Если коэффициент псевдовязкости выбран согласно (39), то величина в квадратных скобках в (43) равномерно ограничена по шагу h. В этом случае последний член в (43) имеет порядок O(t) и не влияет на устойчивость разностной схемы (40). Первые два члена в правой части уравнения (43) для обеспечения условия устойчивости разностной схемы (40) приводят к условию, аналогичному условию Куранта:

.

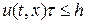Схема (40) является примером так называемой однородной разностной схемы для решения задач с произвольным числом движущихся разрывов, число которых может меняться со временем. Отметим, что помимо псевдовязкости уравнения (35), применяют также псевдовязкость, именуемую линейной. Она имеет следующий вид:

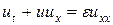, (44)

где 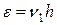, n₁ = const. Уравнение (44) напоминает уравнение теплопроводности все решения которого достаточно гладкие.

Для уравнения (44) определим явную разностную схему вида:

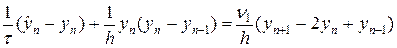. (45)

Проведем сравнительный численный анализ схем (40) и (45). На листинге_№10 приведен код соответствующей программы расчета образования ударной волны по схемам (40) и (45).

Листинг_№10

%Программа сравнения разностных схем (40), (45)

%на примере динамики образования ударной волны

%Очищаем рабочее пространство

clear all

%Задаем пределы области интегрирования G=[0,T]x[0,a]

T=4; a=2;

%Задаем параметры сетки по времени и пространству

tau=0.001; h=0.01; r=tau/h;

%Определяем параметры псевдовязкости схем (40), (45)

nu=1; nu1=0.1;

%Задаем сетки по времени и пространству

t=0:tau:T; x=0:h:a;

Nt=length(t); Nx=length(x);

%Определяем левое граничное условие u(t,0)=0

for m=1:Nt

y(m,1)=0;

end

%Определяем правое граничное условие u(t,0)=0

for m=1:Nt

y(m,Nx)=0;

end

%Определяем начальное условие u(0,x)=sin(pi x)^2,

%0<=x<=1; u(0,x)=0, 1<x<=2

for n=1:Nx

if x(n)<=1

y(1,n)=sin(pi*x(n))^2;

else

y(1,n)=0;

end

end

%Организуем цикл расчета по схеме (40) на различные

%моменты времени

for m=1:(Nt-1)

for n=2:(Nx-1)

y(m+1,n)=(1-r*(y(m,n)-y(m,n-1)))*y(m,n)-...

0.5*r*nu^2*(y(m,n+1)-y(m,n-1))*...

(y(m,n+1)-2*y(m,n)+y(m,n-1));

end

end

%Рисуем профили волны в различные моменты времени на

%одном и том же графике в координатах решение -

%пространственная координата

for m=1:35:Nt

subplot(1,2,1);

plot(x,y(m,:));

hold on

end

%Организуем цикл расчета по схеме (45) на различные

%моменты времени

for m=1:(Nt-1)

for n=2:(Nx-1)

y(m+1,n)=(1-r*(y(m,n)-y(m,n-1)))*y(m,n)+...

r*nu1*(y(m,n+1)-2*y(m,n)+y(m,n-1));

end

end

%Рисуем профили волны в различные моменты времени

for m=1:35:Nt

subplot(1,2,2);

plot(x,y(m,:));

hold on

end

Итоговый результат работы кода листинга_№10 представлен на рис.14. Слева на рис.14 приведены профили волны на различные моменты времени, рассчитанные по разностной схеме (40). Жирными линиями на графике выделено начальное распределение и уже сформировавшаяся ударная волна в последний момент времени. Заметно, что ударная волна слегка размазана в соответствии с выбором величины параметра n. Аналогичная картина представлена на рис.14 справа, где приведены результаты расчета по “линейной” разностной схеме (45). Визуальное сравнение левого и правого рисунков показывает их неплохое совпадение. Это удалось добиться за счет подбора параметра n₁.

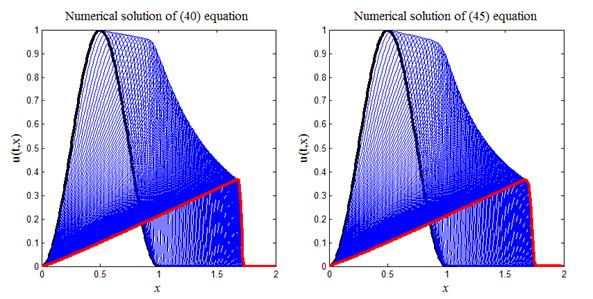
Рис.14. Изучение механизма образования ударной волны на примере
решения квазилинейного уравнения переноса с помощью
разностных схем (40), (45)

Консервативные схемы. В условиях высокой степени неопределенности процедуры составления разностных схем, одним из важнейших свойств, которым может удовлетворять схема является свойство консервативности — следствие того или иного закона сохранения.

Рассмотрим закон сохранения на примере уравнения переноса, записанного в дивергентной форме (33). Выберем некоторую ячейку сетки и проинтегрируем по ней уравнение (33), тогда получится следующее точное интегральное соотношение:

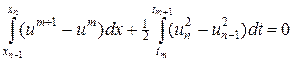. (46)

Уравнение (33) можно проинтегрировать по всей области G(t,x) = [x₀,x_N]´[t₀,t_M] и получить выражение, аналогичное (46), т.е.

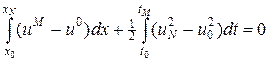. (47)

Уравнение (47) напоминает физический закон сохранения, где первый интеграл описывает изменение величины 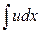за истекшее время, а второй интеграл есть разность потоков 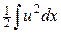через правую и левую границы области G. Выражение (47) является законом сохранения для квазилинейного уравнения переноса (28). Аналогично можно рассматривать уравнение (46) в качестве закона сохранения, но для отдельной ячейки, где также есть сохраняемая величина 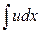и потоки 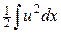на соответствующих границах. Просуммируем теперь уравнение (46) по всем ячейкам области G, тогда

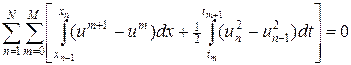. (48)

Совершенно очевидно, что интегралы по внутренним границам области G взаимно уничтожаются и остаются интегралы только по наружным границам, т.е. приходим к закону сохранения в форме (47). Таким образом, закон сохранения во всей области есть следствие закона сохранения в отдельных ячейках.

Не всякая разностная схема обладает таким свойством. Схемы, в которых закон сохранения во всей области является следствием закона сохранения в отдельных ячейках, называются консервативными. Если в некоторой схеме разностный закон сохранения нарушается во всей области G, то такую схему называют неконсервативной.

Построим некоторые примеры консервативных схем. Аппроксимируем интегралы в (47) по формулам прямоугольника©, тогда получим явную схему следующего вида:

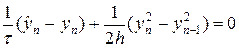. (49)

Консервативность разностной схемы (49) проверяется непосредственно суммированием по m и n, т.е.

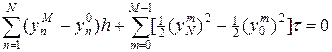. (50)

Выражение (50) является конечно-разностной аппроксимацией закона сохранения в форме (47).

Можно построить и другие консервативные разностные схемы, выбирая различные шаблоны. Например, следуя шаблону рис.2,в, можно получить консервативную неявную схему бегущего счета:

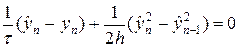. (51)

Решая квадратное уравнение (51) относительно 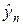и выбирая положительное значение корня, находим

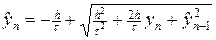. (51¢)

Построены также схемы, которые удовлетворяют многим законам сохранения. Такие схемы называют полностью консервативными.

Изучим схемы (49), (51¢) на предмет описания процесса образования ударной волны. На листинге_№11 приведен код соответствующей программы.

Листинг_№11

%Программа сравнения разностных схем (49), (50')

%на примере динамики образования ударной волны

%Очищаем рабочее пространство

clear all

%Задаем пределы области интегрирования G=[0,T]x[0,a]

T=3; a=3;

%Задаем параметры сетки по времени и пространству

tau=0.002; h=0.01; r=tau/h;

%Задаем сетки по времени и пространству

t=0:tau:T; x=0:h:a;

Nt=length(t); Nx=length(x);

%Определяем левое граничное условие u(t,0)=0

for m=1:Nt

y(m,1)=0;

end

%Определяем начальное условие u(0,x)=sin(pi x)^2,

%0<=x<=1; u(0,x)=0, 1<x<=a

for n=1:Nx

if x(n)<=1

y(1,n)=sin(pi*x(n))^2;

else

y(1,n)=0;

end

end

%Организуем цикл расчета по схеме (49) на различные

%моменты времени

for m=1:(Nt-1)

for n=2:Nx

y(m+1,n)=y(m,n)-r*(y(m,n)^2-y(m,n-1)^2);

end

end

%Рисуем профили волны в различные моменты времени на

%одном и том же графике в координатах решение -

%пространственная координата

for m=1:35:Nt

subplot(1,2,1);

plot(x,y(m,:));

hold on

end

%Организуем цикл расчета по схеме (50') на различные

%моменты времени

for m=1:(Nt-1)

for n=2:Nx

y(m+1,n)=-1/r+sqrt(1/r^2+(2/r)*y(m,n)+y(m+1,n-1)^2);

end

end

%Рисуем профили волны в различные моменты времени

for m=1:35:Nt

subplot(1,2,2);

plot(x,y(m,:));

hold on

end

На рис.15 приведен итог работы кода программы листинга_№11. Образовавшиеся ударные волны довольно сильно отличаются друг от друга при расчетах по схеме (49) (левый график на рис.15) и по схеме (51¢) (правый график на рис.15). Отличия связаны с разными амплитудами ударных волн и с разной скоростью их распространения. Отметим, что таких явных отличий для ударных волн на рис.14, полученных по схемам (40), (45), не просматривается.

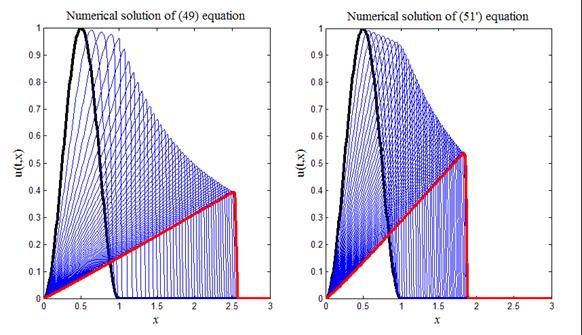
Рис.15. Изучение механизма образования ударной волны на примере
решения квазилинейного уравнения переноса с помощью
разностных схем (49), (51¢)

© Устойчивость называется безусловной, если ее определение выполняется при произвольном соотношении шагов по различным переменным (при условии достаточной малости шагов). Если определение устойчивости обеспечивается дополнительным соотношением, то устойчивость называется условной.

© Это довольно грубые схемы аппроксимации интеграла по формулам: 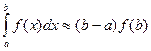, 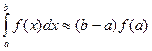. На равномерной сетке эти схемы дают первый порядок точности O(h).