Волновые функции и уравнение Шредингера
В МЭ приборах поведение электрона определяется как поведение элементарной частицы, которая имеет вполне определенный импульс и энергию. Такие частицы двигаются по траекториям, которые можно рассчитать с помощью уравнения Ньютона (TV трубка).
В НЭ приборах поведение электрона основывается на иных принципах. Главная особенность квантово-механического описания электрона состоит в том, что электрон, оставаясь частицей, подобен волне (принцип де Бройля). При этом его пространственные координаты и величину импульса невозможно определить с высокой точностью, т.е. невозможно предсказать направление, если известно, что в данный момент он расположен в какой-либо области пространства.
Что еще более важно: поведение электрона теряет детерминированный характер, т.е. если в некоторый момент времени частица находилась в ограниченной области пространства, то в будущем невозможно достоверно предсказать ее местонахождение. Можно говорить лишь о распределении частиц в пространстве, о вероятности обнаружить ее в заданном месте. Величина, описывающая это распределение, называется волновой функцией частицы.
Т.е. волновая функция – это функция которая задает вероятностное статистическое описание местонахождения электрона в пространстве.
Интенсивность этой функции, а точнее квадрат ее модуля определяет вероятность обнаружения частицы в той или иной области.
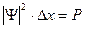 - вероятность нахождения частицы.
- вероятность нахождения частицы.
Волновая функция – основная характеристика наноэлементов. Она содержит в себе полную информацию об электроне или др. частицах в отдельно взятом атоме или молекуле, а также в целом по всему кристаллу.
В общем случае уравнение Шредингера имеет вид:
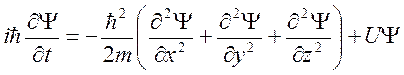 , (1)
, (1)
где m- масса частицы,
U- потенциал поля, в котором движутся частицы.
Его решение – комплексно-значная функция. Хотя сама функция не имеет физического смысла, ее произведение на комплексно-сопряженное число 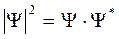 представляет реальную величину, а именно вероятность обнаружения частицы в элементе объема
представляет реальную величину, а именно вероятность обнаружения частицы в элементе объема
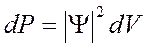
Есть объем, в котором находятся все частицы.
Если проинтегрировать эту функцию по всему объему, то получимусловие нормировки уравнения Шредингера:
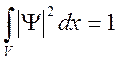
Если U не зависит от времени, то решение этого уравнения можно записать в виде
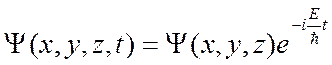
А стационарное уравнение Шредингера (не зависящее от времени) примет вид
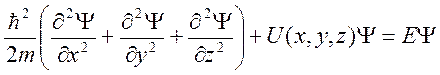 .
.
Дата добавления: 2016-04-14; просмотров: 1098;
