Основные свойства энергетического спектра электрона, находящегося в квантовой яме

1. Минимальная энергия, которой электрон обладает в потенциальной яме, отлична от нуля.

2. С ростом n расстояние между уровнями увеличивается.

3. Чем меньше размер ямы (т.е. меньше область локализации электрона), тем больше расстояние между уровнями.

4. При бесконечно большой ширине ямы (L →∞) дискретный спектр энергии становится сплошным.

Волновые функции

,

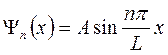чтобы найти А, воспользуемся условиями нормировки:

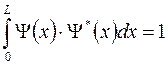, т.е. найдем интеграл от функции

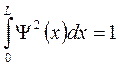
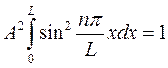, решив, получим

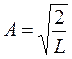, тогда

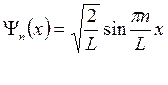- это есть уравнение стоячих волн или уравнение струны (см. рис.*).

В том случае, если потенциальная яма неодномерная и прямоугольная (локализация электронов двумерная и потенциальные барьеры прямоугольные с размерами L и W), то результаты можно обобщить следующим образом:

Волновая функция запишется как суперпозиция волновых функций вида:

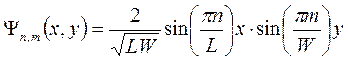, а энергия будет квантоваться:

.

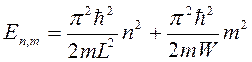Если L=5нм, m_e=10^-27г, то Е₁=0.02 эВ для свободного электрона.

Для электрона, находящегося внутри полупроводника m_e=10^-26г, Е₁=0.2 эВ.