Электроны в прямоугольной яме

Для упрощения задачи рассмотрим поведение электрона в потенциальной яме с бесконечными потенциальными стенками. Такое поведение электрона имеет место в тонких полупроводниковых и металлических пленках, т.к. работа выхода электронов из Ме и ПП порядка 4-5 эВ, а kT=0.0259 эВ.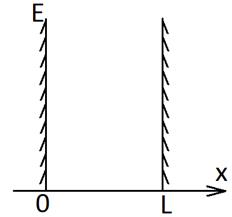

0 0≤x≤ U= ∞ x<0, x>L,

тогда вероятность обнаружить электрон за пределами ямы равна 0, и соответственно волновая функция вне ямы тоже равна нулю.

Из условия непрерывности волновой функции на границах ямы следует, что в точках х=0 и х=L должно быть

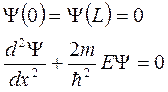- волновая функция, которую необходимо найти для решения этой задачи.

где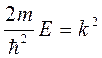

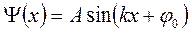
из первого условия ( 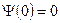) вытекает, что 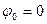, а из второго ( )

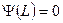sin =0 при 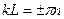, тогда .

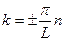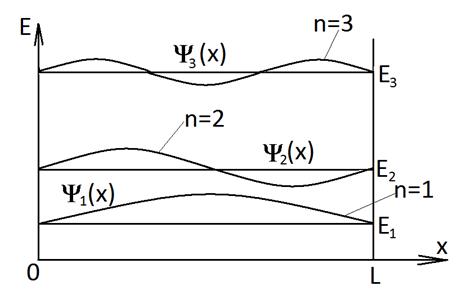
Т.о. мы доказали, что волновое число k (т.е. импульс электрона) в прямоугольной квантовой яме может принимать только дискретные значения. И, следовательно, энергетические уровни, занимаемые электронами в прямоугольной квантовой яме, также могут принимать только дискретные значения. Это следует из закона дисперсии:

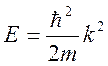, тогда

(*),

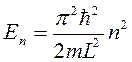где n – главное квантовое число.