Электроны описываются законами идеального газа
n = 1028 – 1029 м-3.
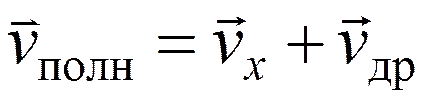
vx – скорость хаотического движения,
vдр – скорость направленного движения электрона (дрейфовая скорость)
Оценим скорости vx и v
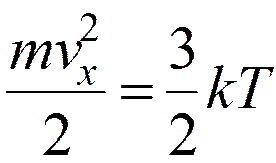
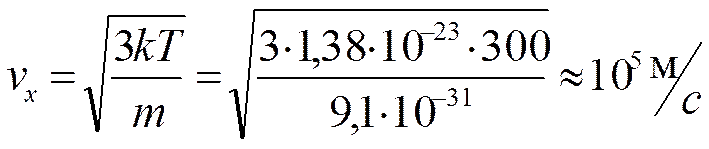
или 100 км/с
j = qnvдр
В медных проводах
j max = 10 A/мм2 = 107 А/м2
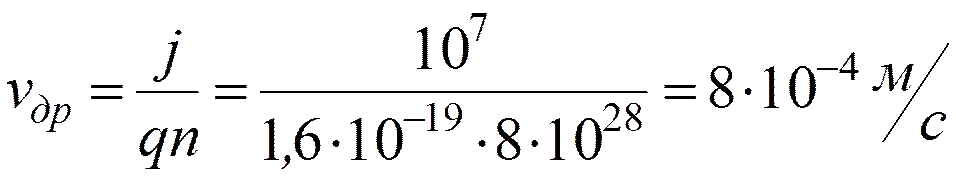
Выведем закон Ома для однородного участка цепи
На электрон в металле (в котором создано и поддерживается электрическое поле) действует сила:
F = q E;
она сообщает ускорение
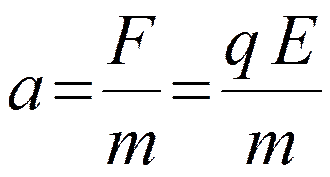 ;
;
Скорость электрона линейно растет и в момент времени t становится равной
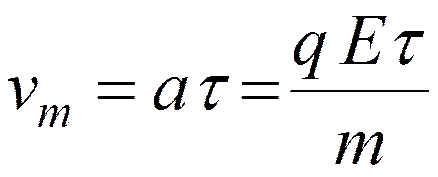 .
.
В этот момент происходит столкновение электрона с узлом кристаллической решетки, электрон отдает энергию решетке, скорость электрона падает до нуля. Далее все повторяется.
t - среднее время между двумя последовательными столкновениями электрона, оно равно
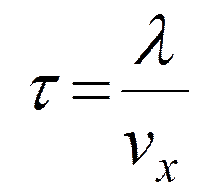 ;
;
Дрейфовая скорость – это средняя скорость направленного движения электрона, она равна половине максимальной:
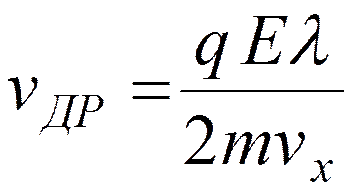
Плотность тока j = qnvдр ;
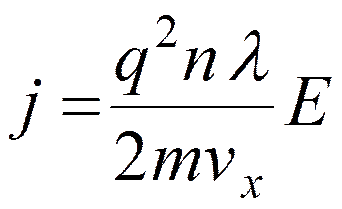
Обозначим 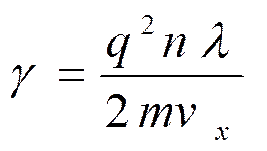
и назовем эту величину удельной проводимостью.
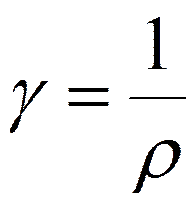 ;
;
1СИ g = 1 См / м;
Тогда для плотности тока получим
j = g Е
Направления векторов плотности тока и напряженности совпадают, тогда
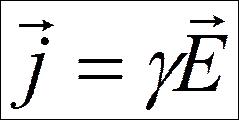
½
закон Ома для однородного участка цепи в дифференциальной форме
Перейдем к интегральной форме закона Ома
Для длинного цилиндрического проводника
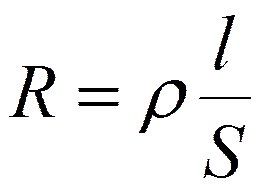

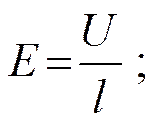
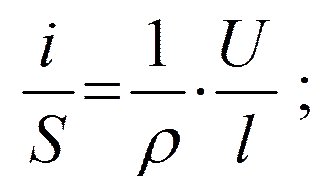
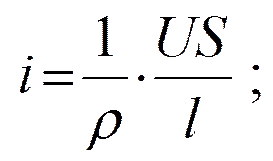 или
или
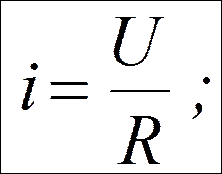
½
закон Ома для однородного участка цепи в интегральной форме
j = qnvдр ;
j = g E;
vдр ~ E
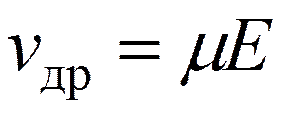 ;
;
m - подвижность электрона
Подвижность носителя заряда – это физическая величина, численно равная средней скорости направленного движения носителя при единичной напряженности электрического поля в проводнике.
1СИm = 1 
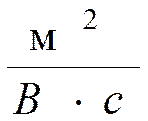
Свяжем удельную проводимость с концентрацией и подвижностью носителей заряда
j = qnvдр ;
j = g E;
В металлах
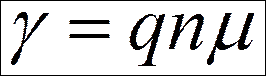 ;
;
В полупроводниках
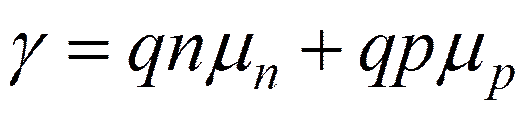
Согласно классической электронной теории металлов
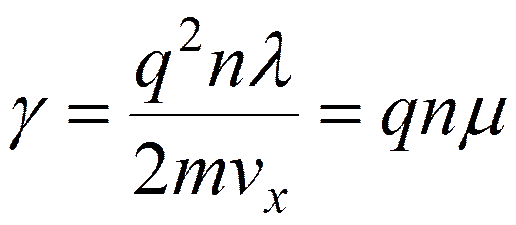
тогда подвижность
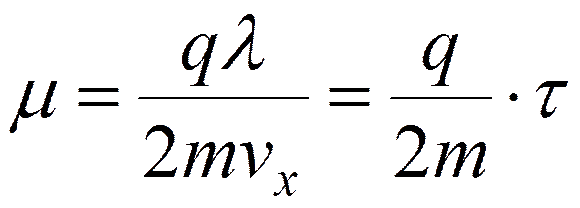
В металлах
m = 10-3 ¸ 10-2 м2/(В.с),
В полупроводниках
m = 10-1 ¸ 1 м2/(В.с)
Таблица. Подвижность электронов в различных материалах при T = 300 К
| Металл | mn, м2/(В×с) | Полупро-водник | mn, м2/(В×с) |
| Ag | 0,0018 | Ge | 0,39 |
| Al | 0,0053 | Si | 0,14 |
| Cu | 0,0080 | InSb | 7,80 |
9. Вывод закона Джоуля-Ленца из классических электронных представлений. Дифференциальная и интегральная формы закона Джоуля - Ленца. Затруднения классической электронной теории.
Удельная тепловая мощность тока
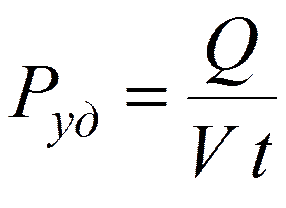
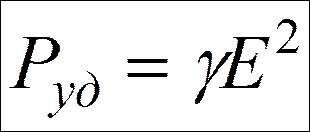
½
дифференциальная форма закона Джоуля – Ленца
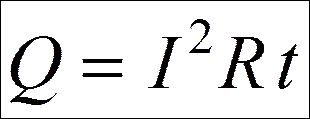
½
интегральная форма закона Джоуля – Ленца
Если ток меняется, то
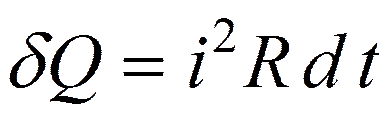 ,
,
тогда
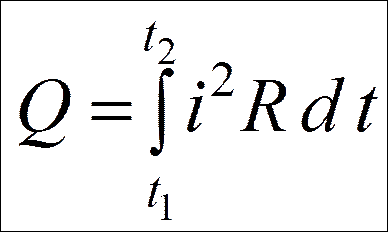
Затруднения классической электронной теории.
Дата добавления: 2016-04-14; просмотров: 822;
