Произвольная квантовая яма

Если потенциальная яма имеет конечную глубину и непрямоуголную форму, то энергия квантования не будет описываться формулой (*).

Но сам вывод о наличии квантования, т.е. о наличии дискретного энергетического спектра остается в силе.

Остается верной и порядковая оценка для энергий квантовых уровней, которую можно получить в общем случае из Гейзенбергского соотношения неопределенности.

Согласно соотношения неопределенности Гейзенберга для энергии:

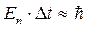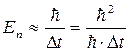, или размытие энергии на временной интервал, т.к.

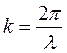, но и 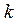~ , а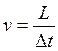

тогда

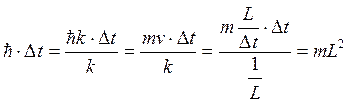(т.к. )

Следовательно:

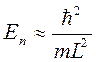???Найти размерность этой величины

Мы знаем, что в произвольной квантовой яме выполняется соотношение

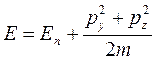
, т.е. картинка, вытекающая из этой формулы имеет вид:

нарисовать

Если нарисовать картинку, как одномерную, то

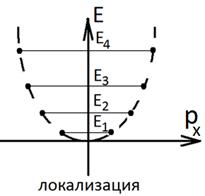
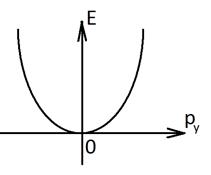
За счет непрерывной компоненты электроны принадлежащие одному и тому же дискретному уровню, могут обладать энергиями от Е_n до ∞.

Такая совокупность энергетических состояний для данного фиксированного n называется подзоной размерного квантования. Для квантовых ям размерность подзон всегда двумерная.