Квантовая механика и теория Бора.

Оптическая микроскопия

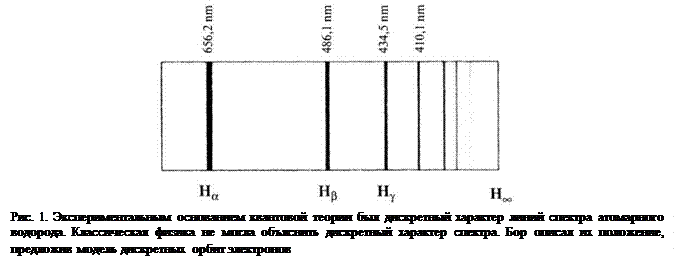
В 1900 году атом представляли как тяжёлое неподвижное положительно заряженное ядро, вокруг которого вращаются лёгкие отрицательно заряженные электроны подобно вращению планет в Солнечной системе. Точное измерение частоты дискретных линий излучения возбуждённого атома водорода (рис. 1) показало, что модель атома нужно пересматривать. Хотя физики написали эмпирические формулы, описывающие линии излучения атома водорода, оставалось непонятным, почему эти линии дискретны. В 1913 году физик Нильс Бор выдвинул два предположения, объясняющих спектр излучения атома водорода:

1. Электроны могут вращаться только на некоторых дискретных орбитах. Эти орбиты имеют различную энергию. Невозбуждённое состояние атома Бор назвал основным.

2. Когда электрон переходит из одного состояния в другое, излучается или поглощается квант света. Частота кванта v даётся формулой:

v = DE/h, (1)

где h – постоянная Планка и DE – разница энергии состояний.

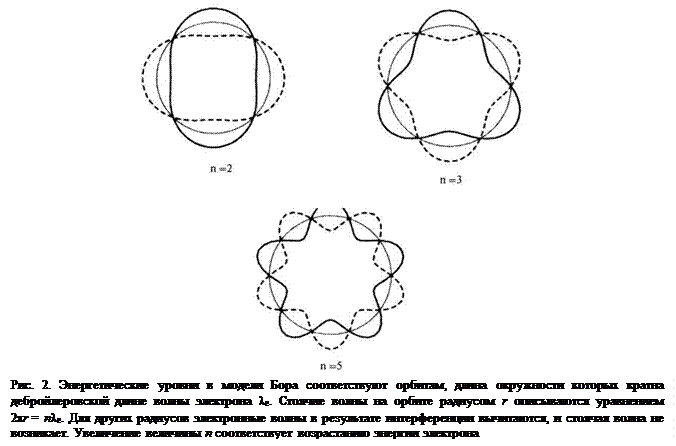
Эти предположения подразумевают, что свет представляет собой поток частиц энергии, названных фотонами. Используя эти постулаты, Бору удалось описать положение линий спектра водорода. Допустимые орбиты аналогичны стоячим волнам в колеблющейся струне. В кандидатской диссертации де Бройль предположил, что электрон является волной, длина которой описывается уравнением l = h/p, где p – импульс электрона. Электрон может оставаться на орбите, только если длина орбиты равна целому числу длин волн, как показано на рис. 2. В противном случае в результате интерференции волны вычлись бы.

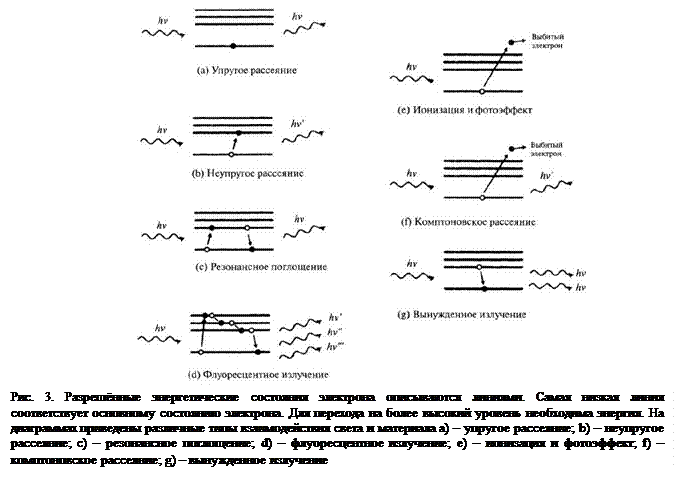
Дискретная природа энергетических уровней приводит к нескольким интересным явлениям, наблюдаемым при взаимодействии фотона с атомом. Пусть фотон имеет частоту v, а его энергия равна hv. Если эта энергия недостаточна для перехода электрона в более высокое энергетическое состояние (рис. 3, а), атом остаётся в основном состоянии, и фотон упруго рассеивается. Если длина волны фотона превышает размер атома, упругое рассеяние описывается классической теорией Рэлея, согласно которой вероятность рассеяния света пропорциональна 1/l⁴.

Если энергия перехода из основного в первое возбуждённое состояние равна DE, а падающий фотон имеет именно такую энергию, происходит резонансное поглощение фотона, и электрон переходит в возбуждённое состояние. Через некоторое время электрон возвращается в основное состояние и испускает фотон, энергия которого равна энергии первичного фотона. Это называют спонтанным излучением. Фаза вторичного фотона не коррелирует с фазой исходного фотона.

Если энергия фотона достаточна для перехода электрона на более высокий энергетический уровень (рис. 3, b), то фотон «неупруго рассеивается» и передаёт атому энергию DE. Частота вторичного фотона v_f не равна энергии первичного фотона:

hv_f = hv – DE. (2)

Этот эффект был впервые описан Раманом и получил название комбинационного рассеяния. В западной литературе его называю рамановским рассеянием. В современной спектроскопии комбинационное рассеяние играет важную роль.

Если энергия фотона превышает DE, то электрон может перейти на второй или более высокий возбуждённый энергетический уровень (рис. 3, c, d). После этого (за время порядка 10^–8с) атом возвращается в основное состояние, проходя через несколько промежуточных состояний. При каждом переходе излучается фотон. Этот процесс называют флуоресценцией. Некоторые атомы и молекулы существуют в возбуждённом состоянии в течение миллисекунд, секунд и даже дольше. В этом случае процесс называют люминесценцией. На этом явлении основана работа экрана электронного осциллографа.

Если энергия фотона ещё выше, электрон может покинуть атом (без испускания фотона), приводя к его ионизации (рис. 3, е). Это явление называют фотоэффектом. Он характеризуется наличием критической энергии фотона, ниже которой фотон не способен выбить электрон. Фотоэффект описывается уравнением:

E_e= hv – W. (3)

Величину W называют работой выхода электрона. Она представляет минимальную энергию, требуемую для выбивания электрона. Если энергия фотона превышает W, выбиваемый электрон имеет энергию E_e. На фотоэффекте основано действие очень чувствительного измерительного устройства – фотоумножителя, схема которого приведена на рис. 4.

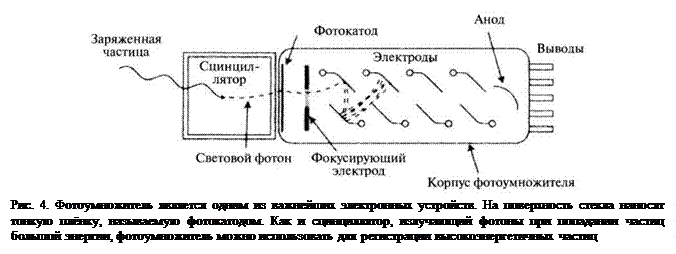Фотон падает на фотокатод, нанесённый на стеклянную подложку, и выбивает из него электрон. Электрон ускоряется электрическим полем в направлении первого электрода (его потенциал выше, чем у катода) и выбивает из него сразу несколько вторичных электронов. Как следствие, количество электронов лавинообразно возрастает по мере движения между соседними электродами вплоть до достижения последнего электрона, называемого анодом. На аноде электроны создают импульс тока, который может быть обработан соответствующей электроникой для определения числа фотонов, попавших на фотокатод. В настоящее время наиболее чувствительные фотоумножители способны регистрировать одиночные фотоны, и некоторые микроскопы имеют специальный режим работы, называемый подсчётом фотонов. Обратим внимание, что в этом режиме работы фотоумножитель является датчиком, измеряющим число фотонов, падающих на его поверхность за некоторый период времени.