Источники электромагнитного излучения.

Космические объекты создают изображение в телескопе, поскольку они или излучают (звёзды), или отражают свет (например, Луна, планеты и искусственные спутники). В материаловедении материалы с естественным свечением практически не встречаются. Поэтому образец нужно осветить, чтобы свет, прошедший через него или отражённый от его поверхности, создал изображение. Освещение образца должно быть однородным.

Раньше единственным источником искусственного света были свечи, и поэтому единицей измерения уровня освещённости довольно долго была «свеча». К настоящей революции в микроскопии привело изобретение электрической лампы, являющейся надёжным и мощным источником света. Освещённость образца можно увеличить, расположив источник в фокусе сферического зеркала.

В современных микроскопах часто используют лазерное освещение. Действие лазера основано на эффекте вынужденного излучения. Если атом находится в возбуждённом состоянии и взаимодействует с фотоном, энергия которого равна разнице энергий возбуждённого и основного состояний атома, может произойти «вынужденный переход». При этом испускаемый фотон имеет одну фазу с первичным фотоном. Если этот процесс происходит в миллиардах возбуждённых атомов, когерентный световой луч постепенно увеличивает свою мощность. Атомы в лазере возбуждают при помощи световой вспышки высокой энергии (рис. 5). Возбуждённый электрон переходит в основное состояние, и излучается фотон с той же частотой и фазой, что и первичный фотон. Эти фотоны многократно отражаются зеркалами, находящимися на торцах лазера. Таким образом, излучение усиливается и создаётся когерентный и коллимированный луч. Одно из зеркал частично прозрачное и пропускает часть падающих фотонов.

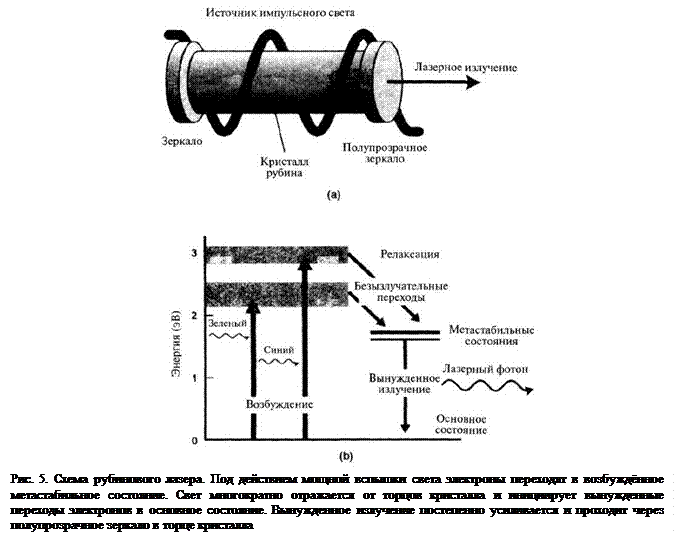
Линзы.

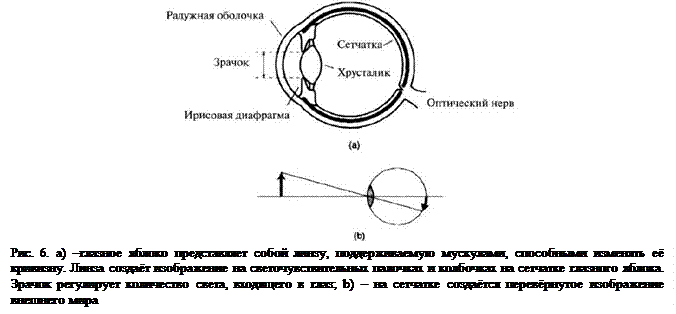
В большинстве микроскопов используются преломляющие линзы. Сначала мы рассмотрим естественную линзу, которой является глаз. На рис. 6 показано поперечное сечение глаза. Мускулы способны изменять кривизну глаза и, как следствие, изменять его фокусное расстояние. Эта способность к аккомодации позволяет нам рассматривать объекты, находящиеся на различных расстояниях от глаза. Спектральная чувствительность глаза определяет видимый интервал электромагнитного спектра (длиной волны от 380 до 760 нм). Анализ лучевых диаграмм показывает, что на сетчатке глаза формируется перевёрнутое изображение внешнего мира. Однако наш мозг обрабатывает его и создаёт прямую (неперевёрнутую) картину мира.

Мелкие объекты видны невооружённым глазом тем лучше, чем ближе они к глазу. Однако глаз не способен создать ясное изображение объекта, если он находится ближе расстояния наилучшего видения, зависящего от возраста человека. Обычно считают, что расстояние наилучшего видения равно 25 см. На этом расстоянии легко различаются объекты размером приблизительно 300 мкм. Чтобы обнаружить более мелкие объекты, нужна увеличивающая линза или микроскоп.

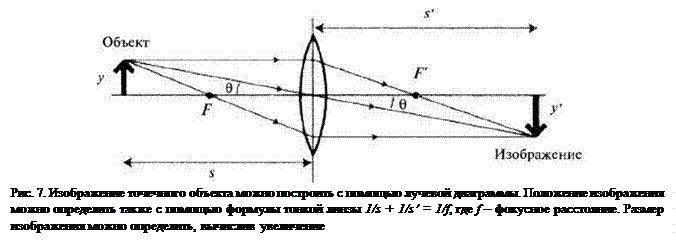
Для построения изображения, формируемого собирающей линзой, можно использовать лучевую диаграмму (рис. 7). Но ещё удобнее это сделать с помощью формулы тонкой линзы. Для тонкой стеклянной линзы эта формула имеет вид:

1/s + 1/s¢ = 1/f = P = (n – 1)(1/r₁ – 1/r₂), (4)

где P – оптическая сила линзы (измеряемая в диоптриях или м^–1), f – фокусное расстояние, s и s¢ – расстояния до объекта и изображения, n – показатель преломления стекла, r₁ и r₂ – радиусы кривизны передней и задней поверхностей линзы. Чтобы эту формулу можно было применять не только для собирающей, но и для рассеивающей линзы, нужно использовать соответствующий знак фокусного расстояния, показанный в табл. 1.

Таблица 1

Знаки тонких линз и сферических поверхностей

В оптической системе изображение может быть действительным или мнимым. Если в плоскость мнимого изображения поместить экран, изображение на нём не появится. Например, изображение нашего лица в зеркале расположено за зеркалом. Однако на экране, помещённом за зеркалом, оно, очевидно, не появляется. Напротив, если в плоскость действительного изображения поместить экран, изображение на нём возникнет. Например, в фотоаппарате фотоплёнку помещают в плоскость реального изображения.

Положение изображения можно найти с помощью лучевой диаграммы, точка пересечения линий которой определяет плоскость изображения. Для линзы нужно рассмотреть три луча. Первый из них параллелен оси, а два других проходят через фокусы линзы. Положительная (собирающая) линза имеет утолщение в её середине, а отрицательная (рассеивающая) – тоньше в середине, как показано на рис. 8.

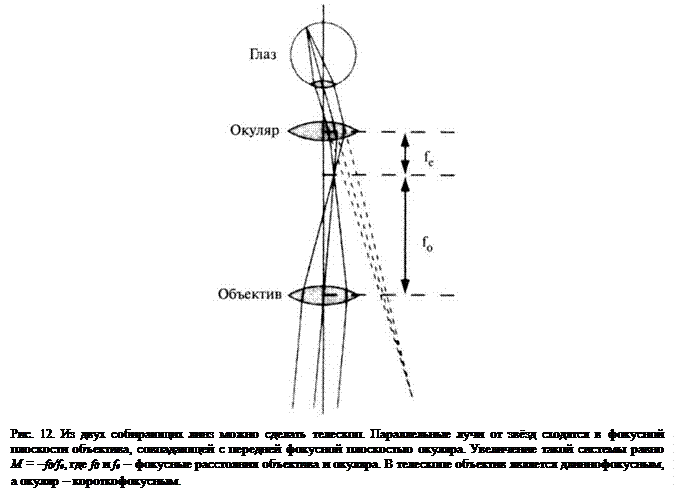
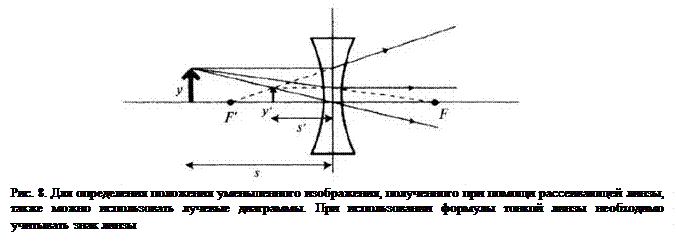Отметим, что линза может быть сложной и состоять из нескольких линз с малым фокусным расстоянием. Такие линзы используют в окулярах микроскопа. Исследуемый объект помещают на фокусном расстоянии от линзы, в результате чего получают увеличенное мнимое изображение, которое рассматривают глазом с расстояния наилучшего видения. Оптическая сила (или поперечное увеличение) характеризует эффективность линзы. Её определяют как отношение угловых размеров изображения и объекта, помещённого на расстоянии наилучшего видения от глаза.

Поперечное увеличение тонкой линзы описывается формулой:

M = y¢/y = s/s¢, (5)

где y¢ и y – размеры изображения и объекта. Отрицательное увеличение означает, что изображение перевёрнуто. Чтобы применять эту формулу для рассеивающих линз, им приписывают некоторый знак (см. табл. 1).

На рис. 9 показано увеличение собирающей линзы в зависимости от расстояния до объекта. Для удобства расстояние от линзы до изображения считали равным расстоянию наилучшего видения. Увеличение линзы описывается формулой:

M = 1 + l_n/f, (6)

где l_n – расстояние наилучшего видения и f – фокусное расстояние линзы.

Геометрическая оптика позволяет построить увеличенное изображение, но не объясняет причины ухудшения его качества в связи с дифракцией света. Чтобы описать разрешение (возможность различить две точки) и контраст изображения, необходимо использовать теорию дифракции.

Разрешение оптического прибора лимитируется дифракцией света. Когда свет, прошедший через небольшое отверстие, проектируется на экран, наблюдается не просто яркое пятно, как в геометрической оптике, а ряд концентрических светлых и тёмных колец вокруг яркого центрального пятна. Если два отверстия поместить близко друг к другу, как на рис. 10, создаваемые ими дифракционные картины накладываются. Размер центрального дифракционного пятна ограничивает пространственное разрешение соседних точек. Дифракция ограничивает разрешение и в случае линзы. Рэлей предложил критерий, определяющий минимальное расстояние d_min между двумя точечными источниками, при котором они всё ещё разрешаются (то есть не сливаются) на экране. Предел разрешения достигается, когда центр дифракционного пятна одного точечного источника накладывается на первое тёмное кольцо дифракционной картины второго источника. Таким образом, разрешающая способность линзы описывается формулой:

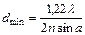, (7)

где l – длина световой волны. Величину nsina называют числовой апертурой линзы.

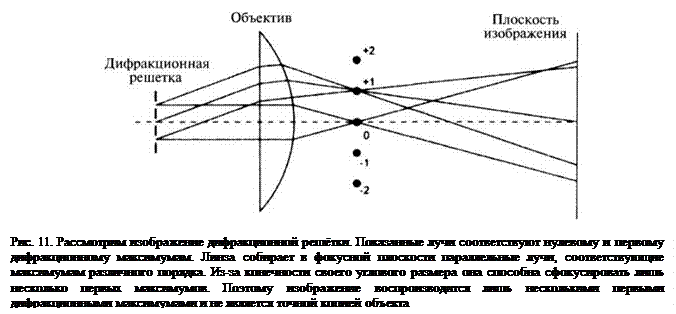
Идеальное воспроизведение объекта ограничено тем, что в объектив микроскопа попадает не весь свет от объекта, а лишь некоторая его часть (рис. 11). Как следствие, некоторая часть информации теряется. Кроме того, для идеального воспроизведения объекта все световые лучи должны пройти одинаковый оптический путь и иметь одинаковую фазу. Поскольку оба этих условия не могут быть выполнены, изображение несовершенно.