Момент силы относительно неподвижной точки и оси

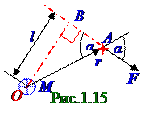
Вектором M_Oмоментаот вектораF силы(рис.1.15) относительно неподвижной О точки, которую называют Ополюсом, равен векторному произведению r радиуса - вектора, проведенного из O точки в A точкуприложения силы, и вектора F силы. Направление вектора M_Oмоментаот вектораF силы, перпендикулярного плоскости, образованной векторами r и F, относительно полюса выбрано таким, чтобы из окончания этого вектора M_Oмомента направление вращения радиуса - вектора r к вектору F силы было видно по кратчайшему расстоянию и против вращения «часовой стрелки». Иначе говорят, что векторы r, F и M_O составляют правую тройку векторов, вследствие чего для этого вектора M_Oмомента имеет место следующее выражение: M₀= [r,F]. (1.56) Модуль M₀ вектора M₀ моментаотвектора F силы имеет следующий вид: M₀ = Frsinα = Fl, (1.57) где α - угол между r и F векторами, а l = rsinα - длина OB перпендикуляра, опущенного из O точки на линию действия вектора F силы. Величина называется lплечом силыотносительно O точки.

Главным моментомот n векторов F₁, F₂, …, F_n сил относительно Ополюса называется вектор M₀, равный геометрической сумме векторов моментов относительно этого Ополюса всех n векторов F₁, F₂, …, F_n сил и имеющий следующий вид: n M_O= ∑[r_i,F_i], (1.58) i = 1

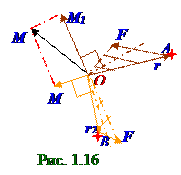
На рис.1.16 вектор M₁ момента от вектора F₁ силы, приложенногок Aточке твердого тела относительно Ополюса,перпендикулярен плоскости, образованной векторами F₁ силы и r₁ радиуса - вектора, и составляют r₁, F₁ и M₁правую тройку векторов. Аналогично вектору M₁ момента от вектора F₁ силы, приложенногок

где r_i_-радиус - вектор, проведенный из Ополюса в точку приложения вектора F силы.

Bточке твердого тела относительно Ополюса, на рис.1.16 построен вектор M₂ момента от вектора F₂ силы относительно Ополюсас учётом, что векторы r₂, F₂ и M₂ составляют правую тройку векторов.

Вектор M₀ главного моментасилы от векторов F₁ и F₂сил относительно Ополюса определён как геометрическая сумма (1.58) вектора M₁момента силы от вектора F₁ силы относительно Ополюса, а также вектора M₂момента силы от вектора F₂ силы относительно того же Ополюса.

направлению и имеют равное l плечоотносительно Ополюса. Поэтому векторы M₁₂ и M₂₁ моментовотвекторов F₁₂и F₂₁ внутренних сил равны по модулю и противоположны по направлению. Их геометрическая сумма равна нулю, вследствие чего с учётом (1.59) имеет место следующее выражение: [r₁,F₁₂] + [r₂,F₂₁] = 0. (1.60)

Векторы моментов (рис.1.17) внутренних силотносительно Ополюса взаимодействия материальных точек системы попарно компенсируются, вследствие чего имеет место следующее выражение: [r_i,F_ik] + [r_k,F_ki] = 0.(1.59) На рис.1.17 на материальные точки с m₁ и m₂массами кроме векторов F₁ и F₂внешних силдействуют также векторы F₁₂и F₂₁внутренних сил притяжения, которые равны по модулю, противоположны по

Следовательно, при вычислении вектора главного моментасил нужно учитывать только векторы F_вн внешних сил, действующих на рассматриваемую механическую систему. На Mматериальную точку (рис.1.18) действует вектор F силы,.

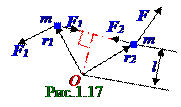
который разложен по i, j, k базису.Векторρj , направленный из начала O координат в Mматериальную точку, перпендикулярен составляющимвектора F, а именно составляющейвектора "-F_Xi" по оси OX координат и составляющейвектора F_Zk по оси OZ координат, поэтому OM отрезок ρ длиной для составляющих векторов "-F_Xi"и F_zk сил являетсяплечомотносительно прямоугольной декартовой системы координат. Векторы M_X i, M_Y j, M_Zkмоментовот векторов"-F_Xi", F_yj и F_zkсилотносительно Ополюса имеют следующий вид:

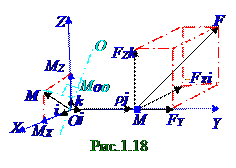
M_Xi = [ρj,F_zk] = iρF_z; M_Zk = [ρj, -F_Xi] = - kρF_X;и M_Y j= 0, (1.61) где F_X - проекция вектора F силы, действующего на Mматериальную точку, на OX ось, имеет отрицательное значение, .к. этот вектор F силынаправлен в сторону, противоположную OX оси.

Вектор F_Yj силынаходится на продолжении OM плечаи его плечо относительно Ополюса равнонулю, поэтому в (1.59) M_Y j = 0. Главныйвектор M₀ моментаот вектора F силыотносительно Ополюсаравен (1.61) геометрической сумме векторов M_Xi и M_Zk моментов от векторов F_zkи"-F_Xi"сил, вследствие чего для этого главноговектора M₀ момента место следующее выражение: M₀ = M_Xi + M_Zk, (1.62) где M_X и M_Z - проекции результирующеговектораM₀ моментасилыот вектора F силыотносительно Ополюсасоответственно на OX и OZ оси.

Относительно (рис.1.18) OZ осик Mматериальной точкеприложен вектор "-F_Xi" силы, имеющий вектор M_Zk момента силы из (1.61). Проекция M_Z момента силы получается из проектирования результирующеговектораM₀моментасилына OZ ось. Поэтому для определения проекции M_O_O' результирующеговектораM₀моментасилыот вектора F силына неподвижную

(рис.1.18) OO' осьсначала определяют этотрезультирующийвекторM₀моментасилы от вектора

F силы относительно любой точки, лежащей на неподвижной OO' оси, а затем проектируют результирующийвекторM₀моментасилы на эту неподвижную OO' ось.

<3 4 567 8 9 >

Дата добавления: 2016-02-14; просмотров: 1293;