Силы, масса в механической системе

Силойназывается векторнаявеличина, являющаяся мерой взаимодействиярассматриваемых тел с другими телами. Взаимодействиеможет осуществляться как между контактирующимителами, например, при трении или ударе, так и между удаленными телами. Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростьюдействия одних частиц на другие называется физическим полемили просто полем. Взаимодействие между удаленными телами осуществляется посредством их гравитационных и электромагнитных полей,например, притяжение планет к Солнцу, взаимодействие заряженных тел, проводников с током.

Вектор F силыопределен, если заданы его модуль F, направление в пространстве и точка приложения. Прямая, вдоль которой направлен вектор F силы, называется её линией действия.

Поле, действующее на материальную точку с вектором F силыназывается стационарным полем, если оно не изменяется с течением t времени, т.е. если в любой точке поля вектор F силы не зависит от времени, т.е. dF/dt = 0.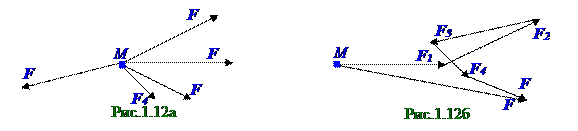

Одновременное действие на Mматериальную точку нескольких векторов F₁,F₂, . . ., F_n (рис.1.12а) сил эквивалентно действию одного вектора F силы, называемого равнодействующимили результирующимвекторомсилы, равного геометрической сумме векторов F₁,F₂, . . ., F_n этих сил и имеющего следующий вид:

n F= ∑F_i.(1.36) i = 1

Вектор (рис.1.12б) F равнодействующейсилы представляет собой замыкающийвектор многоугольника, например, векторов F₁,F₂, . . ., F₅ сил, который строят последовательным параллельным переносом этих векторов F₁,F₂, . . ., F₅ сил, для чего сначала совмещают окончание вектора F₁ силы с началом вектора F₂силы. Потом параллельно переносят вектор F₃силы и прикладывают его к окончанию вектора F₂ силы. Затем повторяют такое же построение (рис.1.12б) с векторами F₄ и F₅, после чего соединяют векторомMматериальную точку с окончанием вектора F₅ силы. Замыкающий многоугольник векторов F₁,F₂, . . ., F₅ вектор F является равнодействующим вектором силы.

Вектор (рис.1.12б) равнодействующей силы можно построить по правилу параллелограмма, т.е. последовательным сложением векторов, приложенных к материальной точке и осуществляющих одновременное действие на эту материальную точку.

Тело называется свободным, если на его положение и движение в пространстве не наложено никаких ограничений. В большинстве случаев приходится иметь дело с телами, которые несвободны:на их возможные положения и движения наложены те или иные ограничения, называемые в механике связями. При изучении поведения несвободныхтел или системы тел в механике пользуются принципом освобождаемости: несвободное тело или систему телможно рассматривать как свободное, заменив действиена него тел, осуществляющих связи, соответствующими силами. Эти силы называютсяреакциями связей, а все остальные силы,действующие натело, - активными силами.

Тела, не входящие в состав исследуемой механической системы, называются внешними телами. Силы, действующие на систему со стороны внешних тел, называются внешними силами. Внутренними силами называются силы взаимодействия между частямирассматриваемой системы. Механическая система называется замкнутой системой, если она не взаимодействует с внешними телами. В классической или ньютоновской механике материальной точкойназывается тело, форма и размеры которого несущественны в условиях данной задачи. Например, движение корабля из одного пункта в другой в первом приближении можно рассматривать как движение материальной точки. Однако в случае необходимости учёта такой «детали» этого движения, как качка корабля при волнении моря, корабль следует рассматривать как протяжённое тело определённой формы. Любое тело или систему таких тел, образующих исследуемую механическую систему, можно рассматривать как систему материальных точек. Для этого все тела механической системынужно мысленно разбить на столь большое число частей, чтобы размеры каждой части были пренебрежимо малы посравнениюс размерамисамих тел.

Массой материальной точкиилимеханической системы называется положительная скалярная величина, являющаяся мерой инертностиэтой материальной точки илимеханической системы.

В ньютоновской механике:

а) масса материальной точки является инвариантнойвеличиной, т.е. не зависит от системы отсчёта;

б) масса - величина аддитивная, т.е. масса системы равна сумме масс всех материальных точек, входящих в состав этой системы;

в) согласно закону сохранения массы, масса замкнутой системы остается неизменной при любых процессах, происходящих в этой системе.

1.1.5 Механическая система и её центр масс. Импульс материальной точки и механической системы

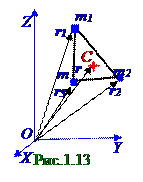
Центром масс системыматериальных точек называется C точка, радиус - вектор r_c которой равен: n

r_c =(∑m_ir_i)/m, (1.37)

i = 1

где m_i и r_i - соответственно масса и радиус - вектор i - ой материальной точки, n - общее число

n

материальных точек в системе, а m = ∑m_i - масса всей системы.

i = 1

На рис.1.13 представлен пример нахождения r_c радиуса - вектора Cцентра масс механической системы, состоящей из 3 -х материальных точек, имеющих m₁, m₂ и m₃ массы с соответствующими r₁, r₂ и r₃ радиусами - векторами. Согласно (1.37) для примера на рис.1.12 выражение для определенияr_c радиуса - вектораCцентра масс механической системыимеет следующий вид: r_c = (m₁r₁ + m₂r₂ + m₃r₃)/(m_{1 +} m₂ + m₃). (1.38)

Подставляем (1.37) в выражение (1.5) связи вектора v мгновенной скорости материальной точкис dr/dt первой производной от радиуса – векторапо t времени рассматриваемой материальной точкии получаем следующее выражение связи вектораv_c мгновенной скорости C центра масс механической системыc суммой векторов m_iv_i импульсов nматериальных точек, из которых состоит эта механическая система: nn v_c = dr_c/dt =(∑m_idr_i/dt)/m=(∑m_iv_i)/m.(1.39)

i = 1 i = 1

Векторная величина p_i, равная произведению m_i массы материальной точки на её вектор v_i скорости, называется импульсомили количеством движения этой материальной точки. Импульсом механической системыматериальных точек называется вектор p, равный геометрической сумме векторов p_i импульсов всех материальных точек системы, вследствие чего имеет место следующее