Работа и кинетическая энергия при поступательном движении механической системы

ЭлементарнойδAработойвектора Fсилы, приложенного к материальной точке, на элементарном перемещения dr называется скалярнаявеличина, имеющая с учетомвыражения(1.5) v= dr/dt связи вектора vмгновенной скорости с первой производной по t времени от r радиуса - векторадвижущейся в (рис. 01.0.1) прямоугольной декартовой системе координат материальной точкойследующий вид: δA = Fdr= Fvdt, (1.80)

где dr- векторэлементарного перемещения материальной точки под действием вектора Fсилы;v- вектор (1.5) мгновенной скорости материальной точки под воздействием вектора Fсилы; dt - элементарный промежуток времени, за который вектор Fсилы совершает элементарнуюδAработу. C учётом разложения (1.46) вектора Fсилы и разложения (1.3) вектора dr элементарного перемещения по базису i,j,k прямоугольной декартовой системы координат, а также с учётом выражения (1.9) связи проекций v_x, v_y, v_z вектора v мгновенной скорости материальнойточки с первыми dx/dt, dy/dt и dz/dt производными перемещения этой материальнойточки по осям прямоугольной декартовой системе координат cкалярное (1.80) Fdr произведение принимает следующий вид:

δA = Fdr = (F_xi +F_y j + F_zk)(idx + jdу+kdz)= F_xdx + F_ydу + F_zdz = (F_xv_x + F_yv_y + F_z v_z)dt, (1.81)

где учтено следующее свойство скалярных произведений координатных ортов: i² =j² = k² = 1, ij = jk = ik = 0.

С учетом равенства (1.7) элементарногоdS приращения пути материальнойточки dr модулю вектора drэлементарного перемещения этой же материальнойточки, т.е. dr = dS, выражение (1.80) принимает следующий вид: δA = Fdr= Fdrcosα = FdScosα = F_rdS,(1.82)

где dS = dr- элементарная длина пути точки приложения силы за рассматриваемый dt малый промежуток времени; α - угол между векторами Fсилы, приложенного кматериальнойточки, и вектором dr элементарного перемещения этой материальнойточки; F_r = Fcosα - проекция вектора F силы на направление вектора dr элементарного перемещения. Если вектор Fсилы, приложенный к материальнойточке, перпендикулярен вектору

dr элементарного перемещения этой материальнойточки, т.е. α = π/2, то согласно (1.82) элементарнаяδAработаравна нулю. Поэтому вектор Fсилы, перпендикулярный вектору dr элементарного перемещенияматериальнойточки, работы не совершает. Вектор F силы называют движущим, если F_r > 0, поэтому δA > 0. Если же F_r < 0, поэтому δA < 0, то вектор F силы называют тормозящим, т.е. силой сопротивления.

Если на материальную точку одновременнодействуют векторы F₁, F₂, …, F_n сил, то элементарнаяδAработа, совершаемая ими за dt малый промежуток времени, равна алгебраическойсумме элементарныхδA_iработа, совершаемых за тот же dt малый промежуток времени каждым из векторов F₁, F₂, …, F_n сил порознь, вследствие чего имеет место следующее выражение:

n n n

δA = ∑δA_i = ∑F_idr_i = ∑F_iv_idt, (1.83) i = 1 i = 1 i = 1 где dr_i- векторэлементарного перемещения материальной точки под действием вектора F_iсилы;v_i- вектор (1.4) мгновенной скорости перемещения на dr длине вектора dr элементарного перемещения материальной точки под воздействием вектора F_i силы.

Подставляем выражение (1.42) второго закона Ньютонаdp = Fdt в (1.80) и получаем следующее выражение, связывающееэлементарнуюδAработу при воздействии на материальную точку, имеющей векторv мгновенной скорости, вектора F силы:δA= vdp, (1.84) где dp - элементарное приращение вектора p импульса материальной точки m массой, которая за элементарный dt промежуток времени приобретает это приращение dpвектора p импульса. Работа внутренних силпри любом движении абсолютно твердого теларавна нулю. При поступательном движениитвердого, имеющего (рис.1.13) Cцентр масс, элементарнаяδAработа(1.80) вектора F_ррезультирующей силыв течение элементарного dt промежутка времени с учетом(1.39) связи v_c = dr_c/dt вектора v_C мгновенной скорости Cцентр масс этого твёрдого тела с первой производной радиуса – вектораdr_C/dt по t времени имеет следующий вид:

δA = F_рdr_c = F_рv_C dt= v_C dp, (1.85)

где (1.51) dp =F_рdt - элементарное приращение вектора p импульса твёрдого тела m массой, центр (1.37) C масс которого за элементарный dt промежуток времени приобретает приращение dpэтого вектора p импульса твёрдого тела.

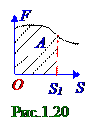
Работа A, совершаемая вектором F силойна конечном участке L траекторииперемещения материальной точки, равна алгебраической сумме (1.80) элементарных δA работ на dr длине вектора dr элементарного перемещения по этой траектории, т.е. с учетом (1.80) выражается следующим криволинейным интегралом: S₁ A = ∫Fdr = ∫F_rdS, (1.86) L 0

Тело, находящееся в состоянии механического движения, обладает W_k кинетической энергией. Элементарноеприращение dW_k кинетической энергии материальной точки равно элементарной δA работе, совершаемойвектором Fсилы на dr длине вектора drэлементарного перемещения этой материальной точки. С учётом выражения (1.85) связи этой элементарнойδAработысвекторомdpэлементарного приращение вектора p импульса материальной точки m массой, а также с учётом выражения (1.42) связи вектораdpэлементарного приращения с вектором dvэлементарного приращения скорости материальной точки m массой элементарноеприращение dW_k кинетической энергии этой материальной точки имеет следующий вид: dW_k= δA = vdp= mvdv = mvdv, (1.87)

где dv-вектор элементарного приращения вектора v мгновенной (1.4) скорости, которое приобрела материальная точка m массойв результате действия вектора F силы в течение элементарного dt промежутка времени.

В ньютоновскоймеханике m = const, поэтому кинетическая энергияW_kматериальной точки m массой в данный момент t времени при достижении телом скорости по модулю, равной v, имеет с учетом (1.87) следующий вид: W_k v

W_k = ∫ dW_к =∫ mvdv = (mv²)/2.(1.88)

0 0

КинетическаяW_kэнергия механическойсистемы равна сумме кинетических энергий всех частейсистемы. КинетическаяW_kэнергия механическойсистемы, состоящей из n материальных точек имеет с учетом (1.88) следующий вид: n

W_k = ∑(m_iv_i²)/2, (1.89) i = 1

где m_i иv_i - соответственно массаи модуль вектора v_i скорости i - ой материальной точки механической системы.

При переходе в (1.89) к dm = ρdV бесконечно малой массе, где соответственно ρ - плотность dV бесконечно малого объем материала твёрдого тела, а dV - бесконечно малый объем с этой dm малой массой, получаем следующее интегральное выражение, с помощью которого определяют кинетическуюW_kэнергию твёрдого тела: W _k =( ∫ρv²dV)/2, (1.90) V

где v- модуль вектора v скорости бесконечно малого dV объематвёрдого тела, а интегрирование ведется по всему V объёму этого твёрдого тела.