Работа и кинетическая энергия при вращательном движении механической системы

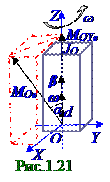
К твёрдому телу (рис.1.21), вращающемуся вокруг OZ оси в произвольный момент t временис с вектором ω угловой скоростии имеющему относительно этой OZ оси момент J_OZ инерции, приложен

(1.58) вектор M_Oвнглавного моментаот всех векторов F внешних сил, приложенных к твёрдому телу

относительно Oполюса, имеющий составляющую вектора M_OZвнпо OZ оси вращения. Элементарная δA работа, выполненная вектором M_Oвнглавного моментасил, при повороте твёрдого тела вокруг OZ оси на вектор dφ бесконечно малого угла приведет к приращению dW _kкинетической энергиитела, которое имеет по аналогии с (1.87) следующий вид: δA= dW_k = M_Oвнdφ=(M_Oвнω)dt = = (M_OZвнω)dt = J_OZβωdt = J_OZ(dω/dt)ωdt = J_OZωdω = J_OYωdω, (1.91) где ω = dφ/dt - вектор ω угловой скоростивращения твёрдого тела вокруг OY оси, равный согласно (1.18) отношению вектора dφэлементарного приращения угла поворота твёрдого телакэлементарному dt промежутку времени, в течение которого длился этот поворот; M_Oвн- вектор главного моментаот всех векторов F внешних сил, приложенных к твёрдому телу относительно Oполюса;

M_OZвн - составляющая вектора M_Oвнглавного момента от всех векторов F внешних сил, приложенных к твёрдому телу, направленная по OZ оси вращения; (M_Oвнω)=M_O_внωcosα и (M_OZвнω) =M_OZ_внω= M_O_внωcosα -равные скалярные произведения, посколькусоставляющая M_OZвн вектора M_Oвн, направленная по OZ оси вращения, определяется из выражения: M_OZвн=M_Oвнcosα, где α -угол между вектором M_Oвни OZ осью;

M_OZвн= J_OYβ - согласно (1.76) уравнению динамики твердого тела вектор M_OZвнглавного момента внешних силпропорционален вектору β углового ускорениявращения твердого тела относительно неподвижнойOZоси;β = dω/dt - вектор β углового ускорениявращения твёрдого тела вокруг OZ оси, равный согласно (1.21) отношению элементарногоприращения вектораdωугловой скорости при вращении твёрдого тела вокруг OZ оси кэлементарному dt промежутку времени, в течение которого это приращения вектораdωугловой скоростипроизошло.dωугловой скорости при вращении твёрдого тела вокруг OZ оси кэлементарному dt промежутку времени, в течение которого это приращения вектораdωугловой скоростипроизошло.

Кинетическая энергияW_k (рис.1.21), вращающегося твёрдого тела вокруг OZоси под воздействием вектора M_Oвнглавного моментаот всех приложенных к твёрдому телу относительно Oполюса векторов F внешних сил, в данный момент t времени, когда модуль вектора ω угловой скоростивращения достигнет ω значения, имеет по аналогии с (1.83) следующий вид:

W_kω W_k=∫ dW_k = ∫ J_OYωdω = (J_OYω²)/2. (1.92) 0 0

<7 8 91011 12 13 >

Дата добавления: 2016-02-14; просмотров: 601;