Сравнение нескольких групп. Критерий Фридмана.
Порядок расчёта.
1. Расположить значения по возрастанию и присвоить ранги для каждого больного в отдельности.
2. Для каждой группы рассчитать сумму рангов.
3. Вычислить экспериментальное значение критерия по следующей формуле:
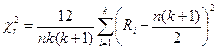 ,
,
где n – число больных; k – число измерений (групп), Ri – сумма рангов в i-ой группе.
4. Сравнить с критическим значением критерия Фридмана (см. приложения) определяемом исходя из численности групп и числа измерений. Если число измерений и численность группы достаточно велико (отсутствует в таблице), можно воспользоваться критическим значением критерия c2 для числа степеней свободы f = k-1.
Пример 5.
Рассмотрим задачу, решенную с помощью дисперсионного анализа повторных измерений.
| Легочное сосудистое сопротивление | До лечения | Через 48 ч | Через 3-6 мес. | |||
| Больной | Значение | Ранг | Значение | Ранг | Значение | Ранг |
| 22,2 | 5,4 | 10,6 | ||||
| 17,0 | 6,3 | 6,2 | ||||
| 14,1 | 8,5 | 9,3 | ||||
| 17,0 | 10,7 | 12,3 | ||||
| Сумма |
Вычисляем экспериментальное значение критерия:
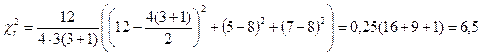 .
.
Критическое значение определяем по таблице (см. приложение): 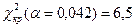 .
.
Экспериментальное значение равно критическому, таким образом, нулевая гипотеза об отсутствии изменения лёгочного сосудистого сопротивления при приёме гидралазина отвергается, с вероятностью ошибки равной 0,042.
Сводная таблица по методам проверки статистических гипотез.
| Количество групп сравнения | Шкала измерения сравниваемых признаков | |||
| Количественная | Порядковая | Качественная | ||
| Независимые выборки (разные люди в сравниваемых группах) | Две группы | Критерий Стьюдента | Критерий Манна-Уитни | Критерий z. Критерий c2. Точный критерий Фишера. |
| Несколько групп | Однофакторный дисперсионный анализ | Критерий Крускала-Уоллиса | Критерий c2. | |
| Зависимые выборки (одни и те же люди в сравниваемых группах) | Две группы | Парный критерий Стьюдента. | Критерий Вилкоксона. | Критерий Мак-Нимара. |
| Несколько групп | Однофакторный дисперсионный анализ повторных измерений. | Критерий Фридмана. |
Правила распространения критериев.
1. По шкалам.
Распространимость справа налево. Критерии для качественной шкалы можно применить и для порядковой и для количественной. Критерии для порядковой шкалы можно применить и для количественной. Критерии для количественной шкалы можно применять только для неё. Это объясняется тем, что количественный признак можно принять и за порядковый и за качественный, но не наоборот.
2. По количеству групп.
Распространимость снизу вверх. Критерии предназначенные для нескольких групп можно применить и для двух групп, но не наоборот.
3. По зависимости выборок.
Распространимость сверху вниз. Критерии предназначенные для независимых выборок можно применить и для зависимых. Но в этом случае мощность критерия может значительно снижаться.
ВЫВОДЫ.
Для сравнения порядковых данных применяют критерии, основанные на рангах, номерах, под которыми будут стоять исходные данные, если их выстроить по возрастанию. Критерии, основанные на рангах, не нуждаются в предположениях о типе распределения.
Аналогом критерия Стьюдента является критерий Манна-Уитни, парного критерия Стьюдента – критерий Вилкоксона, дисперсионного анализа – критерий Крускала-Уоллиса и дисперсионного анализа повторных измерений – критерий Фридмана.
Если отдельные значения встречаются несколько раз, то они заменяются рангами, вычисляемыми как среднее тех мест, которые делят между собой эти значения. При наличии совпадающих значений, как правило, изменяется экспериментальное значение критерия.
[1] В [Гланц С., с.333] ошибочно приведена формула 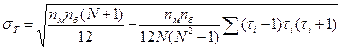 . См. также Справочник по прикладной статистике. В 2-х т.: Пер. с англ./ Под ред. Э.Ллойда, У.Ледермана, Ю.Н.Тюрина.- М.: Финансы и статистика, Т. 2: 1990. - с.130.
. См. также Справочник по прикладной статистике. В 2-х т.: Пер. с англ./ Под ред. Э.Ллойда, У.Ледермана, Ю.Н.Тюрина.- М.: Финансы и статистика, Т. 2: 1990. - с.130.
Дата добавления: 2016-02-04; просмотров: 1828;
