Сравнение нескольких групп. Критерий Крускала-Уоллиса.

Порядок расчёта.

1. Данные всех групп объединяют и упорядочивают по возрастанию. Ранг 1 присваивается наименьшему из всех значений, ранг (n₁+n₂+…+n_k) – наибольшему. Совпадающим значениям ранги присваиваются как среднее тех мест, которые делят между собой эти значения.

2. Для каждой группы вычисляют сумму рангов .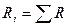

3. Экспериментальное значение критерия определяется по следующей формуле:

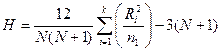где N = n₁+n₂+…+n_k – общее число наблюдений;

R_i – сумма рангов в i-ой группе;

k – число групп.

4. Экспериментальное значение сравнивается с критическим, определяемым по таблице критических значений распределения Крускала-Уоллиса, исходя из требуемого уровня значимости и численности групп. В приложениях приведены критические значения для трёх групп численностью не превосходящей 6. При достаточно большой численности групп распределение H близко к распределению c², поэтому, H надо сравнить с критическим значением распределения c² для числа степеней свободы, равное f = k-1.

В случае трёх групп приближение с помощью c² пригодно, если численность каждой группы не меньше 5. Для четырёх групп – если общее число наблюдений не менее 10.

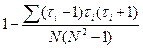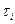При большом числе совпадающих рангов значение H следует поделить на , где - число значений i-го ранга, суммирование производится по всем совпадающим значениям.

Пример 3:

Дополним первый пример данными ещё двух групп по такому же показателю.

1 группа (n₁ =5)	2 группа (n₂ =4)	3 группа (n₃ = 4)	4 группа (n₄ = 5)
Показатель	Ранг	Показатель	Ранг	Показатель	Ранг	Показатель	Ранг
					5,5
	5,5
	5,5
			5,5

Сумма			33,5		44,5

Наименьшее значение 1, в объединённой группе три человека имеют это значение. Значит, у каждого средний ранг будет: (1+2+3)/3 = 2. Далее на 4, 5, 6 и 7 местах располагаются значения показателя равные 2, следовательно, средний ранг будет (4+5+6+7)/4 = 5,5. И, наконец, для людей со значением показателя равным 3 ранг составит – (8+9+10+11+12+13+14+15+16+17+18)/11 = 13.

Вычисляем экспериментальное значение критерия: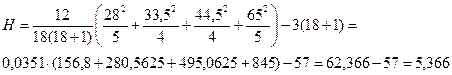

В нашем случае много совпадающих значений (1 – 3 раза; 2 – 4 раза; 3 – 11 раз), поэтому уточняем значение H с учётом этого:

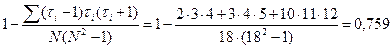
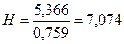
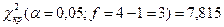Экспериментальное значение меньше критического, таким образом, нулевую гипотезу о равенстве показателя в сравниваемых группах отвергнуть нельзя.

Зависимые выборки.

<14 15 16 171819 20 >

Дата добавления: 2016-02-04; просмотров: 950;