Сравнение двух групп. Критерий Манна-Уитни.
Порядок расчёта.
1. Данные обеих групп объединяют и упорядочивают по возрастанию. Ранг 1 присваивается наименьшему из всех значений, ранг (n1+n2) – наибольшему. Если значения совпадают им присваивают один и тот же средний ранг (например, 3 и 4 место – ранг (3+4)/2 = 3,5; 6,7,8 место – ранг (6+7+8)/3 = 7).
2. Для меньшей группы вычисляют Т – сумму рангов её членов. Для Т-критерия Манна-Уитни она и будет являться экспериментальным значением критерия. Для U-критерия вычисляют 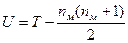 , где nм – численность меньшей из групп.
, где nм – численность меньшей из групп.
3. Экспериментальное значение сравнивается с критическими, определяемым по соответствующим статистическим таблицам, исходя из требуемого уровня значимости и численности групп. Если экспериментальное значение меньше или равно первому критическому или больше либо равно второму, то нулевая гипотеза отвергается.
В таблице критических значений критерия Манна-Уитни приведены значения для численностей групп до 8 человек. При численности групп больше 8, распределение Т приближается к нормальному со средним
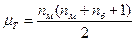
и средним квадратическим отклонением
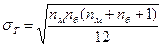 , где nм и nб – численность меньшей и большей групп.
, где nм и nб – численность меньшей и большей групп.
Если некоторые значения совпадают, стандартное отклонение должно быть уменьшено согласно формуле:
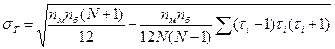 , [1]
, [1]
где 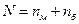 ,
, 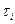 - число значений i-го ранга, а суммирование проводится по всем совпадающим рангам.
- число значений i-го ранга, а суммирование проводится по всем совпадающим рангам.
В таком случае величина
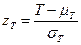 (с поправкой Йейтса на непрерывность
(с поправкой Йейтса на непрерывность 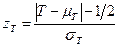 )
)
имеет нормированное нормальное распределение (со средним 0 и средним квадратическим отклонением 1). Это позволяет сравнить zT с критическими значениями нормального распределения: 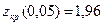 ,
, 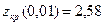 ,
,  .
.
Пример 1:
Данные по сравниваемым группам приведены в следующей таблице. Сравниваемый показатель порядковый, принимает три возможных значения: 1 – низкое; 2 – среднее; 3 – высокое.
| 1 группа (n1 = 5) | 2 группа (n2 = 4) | ||
| Показатель | Ранг | Показатель | Ранг |
| Сумма |
Наименьшее значение 1, в объединённой группе три человека имеют это значение. Значит, у каждого средний ранг будет: (1+2+3)/3 = 2. Далее на 4, 5 и 6 местах располагаются значения показателя равные 2, следовательно, средний ранг будет (4+5+6)/3 = 5. И наконец, для людей со значением показателя равным 3 ранг составит – (7+8+9)/3 = 8.
Сумма рангов для наименьшей по численности группе (это группа 2) равна 23, т.е. Тэксп = 23.
По таблице критических значений находим: Ткр1 (nм = 4, nб = 5, a = 0,063) = 12; Ткр2 (nм = 4, nб = 5, a = 0,063) = 28.
Для того, чтобы отвергнуть нулевую гипотезу экспериментальное значение должно быть либо меньше первого критического значения, либо больше второго. В нашем случае, Ткр1 < Тэксп < Ткр2, таким образом нулевую гипотезу об отличии сравниваемых групп отвергнуть нельзя.
Пример 2.
В исследовании когнитивных функций, рассмотренном в «описательной статистике» 32 ребёнка представляли контрольную группу, 40 экспериментальную. Сравнить две группы по времени выполнения задания.
Данные представлены в таблице:
| Время выполнения 1-го задания по табл. Шульте, с | |||||||||||||||||
| Контрольная группа | |||||||||||||||||
| Экспериментальная группа |
При описании данных контрольной группы было получено несимметричное распределение показателя. Кроме того, показатель измерен достаточно грубо, с точностью до 5 с, соответственно возможных значений будет немного. Поэтому для сравнения воспользуемся критерием Манна-Уитни. Расчет рангов представлен в таблице:
| Время выполнения 1-го задания по табл. Шульте, с | |||||||||||||||||
| Контрольная группа | |||||||||||||||||
| Экспериментальная группа | |||||||||||||||||
| Накопленные частоты | |||||||||||||||||
| Ранг | 26,5 | 38,5 | 51,5 | 55,5 | 66,5 | 68,5 | 71,5 | ||||||||||
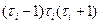
|
Для определения рангов воспользуемся накопленными частотами, показывающими общее количество данных в данной ячейке и во всех предыдущих по обеим группам (данные объединяются при вычислении рангов). По ним видно, какие места будут занимать соответствующие значения. Итак, минимальное значение 30 имеет в объединённой группе 1 человек, соответственно присваиваем ему ранг 1, следующее значение 35 – также один человек – ранг 2. Следующее значение 40 имеет 5 человек, накопленная частота в этой ячейке 7, предыдущее значение 2, следовательно, места, которые они занимают - 3,4,5,6,7 и средний ранг для этого значения (3+4+5+6+7)/5 = 5. Аналогично, ранг для значения 45 – (8+9+10)/3 = 9; ранг для значения 50 – (11+12+13+14+15+16+17+18+19+20+21+22+23)/13 = 17 и так далее.
Вычисляем сумму рангов для меньшей по численности, т.е. контрольной группы с учётом повторяющихся значений:
Т = 1*1+2*1+5*3+9*1+17*4+26,5*2+32*5+38,5*3+46*3+51,5*3+ 55,5*1+60*1+64*1+66,5*1+68,5*1+71,5*1 = 1102.
Численность групп больше 8, поэтому для проверки нулевой гипотезы перейдём от Т к zT.
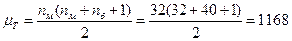 .
.
Среднее квадратическое отклонение вычисляем с учётом совпадающих значений, в этом случае в формулу входит 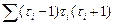 , где
, где 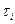 - число значений i-го ранга, суммирование производится по всем совпадающим рангам. Таким образом, для всех частот больших в объединённой группе (повторяющиеся ранги) вычислим произведение
- число значений i-го ранга, суммирование производится по всем совпадающим рангам. Таким образом, для всех частот больших в объединённой группе (повторяющиеся ранги) вычислим произведение 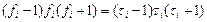 и запишем результат в общей таблице. Для частоты 3, например это будет (3-1)*3*(3+1)=2*3*4=24.
и запишем результат в общей таблице. Для частоты 3, например это будет (3-1)*3*(3+1)=2*3*4=24.
Итак, 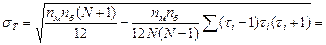
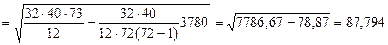
Как видим, совпадающие значения уменьшают среднее квадратическое отклонение незначительно.
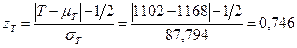 .
.
Критическое значение для уровня значимости 0,05 – 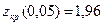 . Таким образом, экспериментальное значение меньше критического и можно считать сравниваемые группы детей не отличающимися по времени выполнения первого задания по таблице Шульте.
. Таким образом, экспериментальное значение меньше критического и можно считать сравниваемые группы детей не отличающимися по времени выполнения первого задания по таблице Шульте.
Дата добавления: 2016-02-04; просмотров: 4786;
