C2 - критерий Пирсона
Критерий применяется в двух случаях:
1) для сопоставления эмпирического распределения признака с теоретическим (равномерным, нормальным или каким-то иным);
2) для сопоставления двух эмпирических распределений одного и того же признака.
Критерий отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух эмпирических распределениях.
Признак может быть измерен по любой шкале, даже номинальной.
Ограничения:
1) n³30;
2) теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f³5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы можем применять метод c2, только накопив определенное минимальное число наблюдений. Так, если количество разрядов (k) задано заранее, минимальное число наблюдений (nmin) определяется по формуле: nmin= 5k
3) выбранные разряды должны «вычерпывать» все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях;
4) необходимо вносить поправку на непрерывность при сопоставлении распределений признаков, которые применяют всего 2 значения. При внесении поправки значение c2 уменьшается;
5) разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может отнесено ни к какому другому разряду.
Вычисление критерия:
1) при сравнении эмпирического с теоретическим равномерным распределением. Для этого лучше воспользоваться таблицей 34.
Таблица 34
| Разряды | fэj | fт | (fэj-fт) | (fэj-fт)2 | (fэj-fт)/fт |
Здесь в 1 столбике даются наименования разрядов,
во 2 столбике даются эмпирические частоты по каждому разряду fэj, где j меняется от 1 до k,
в 3 столбике теоретическая частота, одинаковая для каждого разряда и вычисленная по формуле fт=n/k,
в 4 столбике находится разность между эмпирической и теоретической частотами по каждому разряду,
в 5 столбике значения 4 столбика возводятся в квадрат по каждому разряду,
в 6 столбике находится отношение значений 5 столбика к теоретической частоте по каждому разряду.
| Эмпирическое значение критерия есть сумма значений 6 столбика, т.е. | 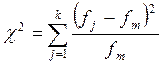
|
Далее находим число степеней свободы по формуле n=k-1 и определяем для данного n критические значения критерия (таблица 5 приложения 2).
Если c2>c20,01, то эмпирическое распределение отличается от равномерного, если c2£c20,05, то эмпирическое распределение не отличается от равномерного, если c20,05< c2£c20,01, то отличие эмпирического распределения от равномерного значимо на 5% уровне.
Таблица 35
Распределение учащихся по когнитивному стилю «дифференциальность-интегральность» и расчет данных по критерию c2
| Стиль | fэмп | fт | (fэмп-fт)2 | (fэмп-fт)2/fт |
| Дифференциально-теоретический | 2,5 | |||
| Дифференциально-деятельностный | 0,4 | |||
| Дифференциально-эмоциональный | 1,6 | |||
| Интегрально- теоретический | 8,1 | |||
| Интегрально- деятельностный | 6,4 | |||
| Интегрально- эмоциональный |
Пример. У учащихся подросткового возраста (60 человек 13-14 лет) выявлялся когнитивный стиль «дифференциальность-интегральность» по методике Г.А. Берулава. В каждом стиле выделяются три стратегии: теоретическая, деятельностная, эмоциональная. Распределение учащихся по стилям представлены в таблице 35. Можно ли утверждать, что в данной группе учащихся равномерно представлены все данные стили?
Решение: n=60 >30, следовательно, применим критерий c2.
Сформулируем экспериментальную гипотезу: распределение учащихся по стилям «дифференциальность-интегральность» с тремя стратегиями является равномерным.
к=6, следовательно, fт=60/6=10.
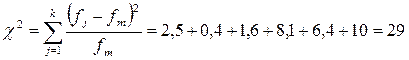
Для n=к-1=6-1=5
c20,05=11,070 c20,01=15,089
c2>c20,01, следовательно, экспериментальная гипотеза отвергается.
Ответ: распределение учащихся по стилям «дифференциальность-интегральность» с тремя стратегиями отличается от равномерного.
2) При сравнении двух эмпирических распределений:
Вычисления также произведем с помощью таблицы 36.
Таблица 36
| нр | fэ1j | fэ2j | fэ1j+fэ2j | fт1j | fт2j | (fэ1j-fт1j)2 fт1j | (fэ2j-fт2j)2 fт2j |
Здесь в 1 столбце записывается наименование разрядов,
во втором столбце записываются соответствующие частоты первого эмпирического распределения (fэ1j), где j меняется от 1 до к,
в третьем столбце записываются соответствующие частоты второго эмпирического распределения (fэ2j),
в 4 столбце находится сумма эмпирических частот первого и второго распределения по каждому разряду отдельно (fэ1j+fэ2j),
| в 5 столбце записывается теоретическая частота каждого разряда первого эмпирического распределения, вычисленная по формуле: | 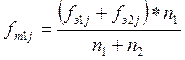 ; ;
|
| в 6 столбце записывается теоретическая частота каждого разряда первого эмпирического распределения, вычисленная по формуле: | 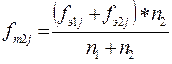 ; ;
|
в 7 столбце находится квадрат разности соответственно эмпирической частоты первого распределения с его теоретической частотой по каждому разряду и делится на эту теоретическую частоту ((fэ1j-fт1j)2/ fт1j),,
в 8 столбце находится квадрат разности соответственно эмпирической частоты второго распределения с его теоретической частотой по каждому разряду и делится на эту теоретическую частоту ((fэ2j-fт2j)2/ fт2j).
Значение критерия есть сумма всех значений 7 и 8 столбцов, т.е.
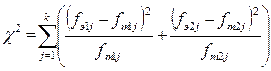 .
.
Далее также находится число степеней свободы n и по таблице 5 приложения 2 находятся критические значения.
Если c2>c20,01, то одно эмпирическое распределение отличается от другого, если c2£c20,05, то первое эмпирическое распределение не отличается от второго, если c20,05< c2£c20,01, то отличие двух эмпирических распределений друг от друга значимо на 5% уровне.
Пример. У учащихся подросткового возраста массовой школы (25 человек) и воспитанников детского дома (25 человек) определялись особенности образа «я» по методике «Каким я кажусь себе». В результате выделилось 7 категорий высказываний о себе. Данные представлены в таблице 36. Различается ли распределение количества высказываний о себе по категориям подростков детского дома и массовой школы?
Решение: n1=88 (количество высказываний подростков массовой школы о себе), n2=111 (количество высказываний подростков детского дома о себе). n1, n2 >30, следовательно, применим критерий c2.
Сформулируем экспериментальную гипотезу: распределение высказываний подростков детского дома и массовой школы о себе по различным категориям существенно отличаются.
Вычислим эмпирическое значение критерия в таблице 37.
Таблица 37
Количество высказываний подростков детского дома и массовой школы о себе и расчет критерия c2
| № катег. выск. | f1 | f2 | f1+f2 | fт1 | fт2 | (f1-fт1)2 fт1 | (f2-fт2)2 fт2 |
| 13,27 | 16,73 | 0,81 | 0,53 | ||||
| 19,45 | 24,54 | 0,33 | 0,26 | ||||
| 8,84 | 11,15 | 1,67 | 1,33 | ||||
| 10,17 | 12,83 | 8,27 | 6,55 | ||||
| 12,38 | 15,62 | 4,69 | 3,72 | ||||
| 15,48 | 19,52 | 0,01 | 0,01 | ||||
| 8,4 | 10,59 | 5,19 | 4,1 |
Категории высказывания:
1) формально-библиографические ролевые сведения; 2) отношения к окружающим людям; 3) отношение к своему возрасту, взрослости, самостоятельности; 4) умения, интересы, способности, интеллект; 5) поведение; 6) качества личности; 7) внешность, отношение к сверстникам противоположного пола.
χ2эмп=0,81+0,33+1,67+8,27+4,69+0,01+5,19+0,53+0,26+1,33+6,55+3,72+0,01+4,1=37,47;
Найдем число степень свободы ν=7-1=6.
Для ν=6 χ20,01=16,812; χ20,05= 12,592.
χ2эмп > χ20,01Þ принимается экспериментальная гипотеза.
Ответ: Количество высказываний о себе, относящихся к разным категориям, у подростков детского дома отличаются от количества высказываний подростков массовой школы.
Поправка на непрерывность вносится тогда, когда n=1. Формула тогда имеет следующий вид:
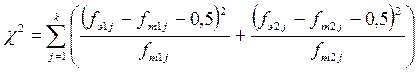 .
.
Пример. У студентов I курса педагогического вуза (факультетов физики и математики, биологии и химии, филологии) выявлялась принадлежность к когнитивному стилю «полезависимость-поленезависимость» по методике «Замаскированные фигуры» Готтшальтда. Результаты исследования представлены в таблице 37. Выявляются ли половые различия в принадлежности к данным стилям?
Решение: n1=49 (количество юношей), n2=53 (количество девушек), n1, n2 >30, следовательно, применим критерий c2.
Сформулируем экспериментальную гипотезу. Юноши и девушки студенты по принадлежности к когнитивному стилю «полезависимость-поленезависимость» различаются.
Найдем эмпирическое значение критерия по таблице 38.
Таблица 38
Распределение девушек и юношей по принадлежности к стилю «полезависимость-поленезависимость» и расчет значения критерия χ2
| Стиль | f1 | f2 | f1+f2 | fт1 | fт2 | (f1-fт1-0,5)2 fт1 | (f2-fт2-0,5)2 fт2 |
| ПЗ | 23,1 | 24,9 | 3,99 | 2,97 | |||
| ПНЗ | 25,9 | 28,1 | 2,86 | 3,28 |
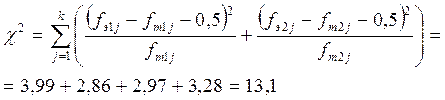
к=2, следовательно, n=1.
Для данного n - χ20,01=6,635; χ20,05= 3,841.
χ2эмп > χ20,01Þ принимается экспериментальная гипотеза.
Ответ: юноши и девушки по принадлежности к когнитивному стилю «полезависимость-поленезави-симость» различаются.
Дата добавления: 2016-01-26; просмотров: 2038;
