U – критерий Манна-Уитни
Критерий непараметрический. Предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественного измеренного. Является более мощным, чем критерий Розенбаума.
В данном критерии определяется, достаточно ли мала зона перекрещивающихся значений между двумя рядами. Чем она меньше, тем более вероятно, что различия между выборками достоверны.
Ограничения критерия: 1) n1,n2³3; 2) n1,n2£60.
Эмпирическое значение критерия вычисляется по формуле:
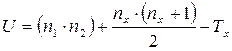
| n1 – количество испытуемых в выборке 1; n2 – количество испытуемых в выборке 2; Tx – большая из ранговых сумм; nx – количество испытуемых в группе с большей суммой рангов. |
Ранговые суммы находятся следующим образом. Упорядочиваются значения 1 и 2 выборки по убыванию. Располагаем их соответственно в 1 и 2 ряды. Далее ранжируем все значения как единую выборку, приписывая минимальному значению наименьший ранг. Следующий шаг - выписываются отдельно ранги 1 и 2 ряда и подсчитывается сумма рангов 1 ряда Т1 и соответственно 2-го ряда – Т2.
Критические значения критерия U можно определить по таблице 2 приложения 2.
Различия между выборками считаются достоверными, если Uэмп£U0,01; незначимыми, если Uэмп>U0,05; достоверными на 5% уровне, если U0,01 <Uэмп £U0,05.
Пример. С учащимися 5 класса (10 человек) и 6 (12 человек) проводился эксперимент на продуктивную классификацию. Предлагалось 10 несвязанных между собой слов. Необходимо было объединить эти слова в группу по какому-то общему признаку (признак необходимо назвать). В группу может входить от двух до 10 слов. Причем одно слово может входить в разные группы. Результаты эксперимента представлены в таблице 17.
Различаются ли учащиеся 5 и 6 классов по показателю продуктивной классификации?
Таблица 17
Результаты исследования продуктивной
классификации учащихся 5 и 6 классов
| 5 класс | 6 класс | ||||||
| № | оценка | № | оценка | № | оценка | № | оценка |
Решение: Данные представлены в интервальной шкале; 3<n1=10 и n2=12 < 60;
Следовательно, для решения данной задачи мы имеем право применять критерий U.
Таблица 18
Упорядоченные индивидуальные значения учащихся 6 и 5 классов по показателю продуктивной классификации и их ранги
| 1 ряд: 6 класс | 2 ряд: 5 класс | Ранги |
| 20,5 | ||
| 17,5 | ||
| 8 8 8 8 | 8 8 | 13,5 |
| 7 7 7 7 | 8,5 | |
| 6 6 6 | ||
| 1,5 |
Для вычисления необходимо упорядочить данные по убыванию. При этом значения выборки, где данные предположительно выше, записываются в 1-й ряд, а где – ниже, соответственно во 2-й ряд. Так, в нашем случае, 1 ряд – значения учащихся 6 класса, 2 ряд – 5 класса (таблица 18).
Сформулируем экспериментальную гипотезу: учащиеся 6 класса превосходят учащихся 5 класса по показателю продуктивной классификации.
Проранжируем все значения как единую выборку, приписывая минимальному значению наименьший ранг (3 столбик таблицы 18). Так, значению 4, как самому наименьшему в обеих выборках, приписывается ранг 1,5, так как и в той и в другой выборке оно встречается по одному разу, а в общей сложности два раза.
Таблица 19
Ранги 1 и 2 рядов по таблице 18
| 1 ряд | 2 ряд | ||
| Частота варианты имеющий этот ранг | Ранг | Частота варианты имеющий этот ранг | Ранг |
| 20,5 | |||
| 20,5 | |||
| 17,5 | 17,5 | ||
| 13,5 | 13,5 | ||
| 8,5 | |||
| 1,5 | |||
| 1,5 |
Выпишем отдельно ранги 1 и 2 ряда (таблица 19) и подсчитаем сумму рангов 1-го ряда Т1= 149,5 и соответственно 2-го ряда – Т2=103,5. Наибольшую ранговую сумму обозначим Тх=Т1=149,5. Следовательно, nx=12. Подставим все значения в формулу критерия и получим Uэмп=48,5. По таблице 2 приложения 2 найдем критические значения критерия для n1=10 и n2=12: U0,01=24, U0.05=34. Uэмп>U0,05Þ экспериментальная гипотеза не подтверждается.
Ответ: Учащиеся 6 класса не превосходят учащихся 5 класса по показателю продуктивной классификации.
Дата добавления: 2016-01-26; просмотров: 2942;
