L - критерий Колмогорова-Смирнова

Критерий применяется в двух случаях:

1) для сопоставления эмпирического распределения признака с теоретическим – равномерным, нормальным или каким-то иным;

2) для сопоставления двух эмпирических распределений одного и того же признака.

Критерий отвечает на вопрос о том, велика ли максимальная разность между накопленными относительными частотами двух распределений.

Ограничения:

1) при сравнении двух эмпирических распределений n_1,2³50, при сравнении эмпирического с теоретическим n³5.

2) разряды должны быть представлены хотя бы в ранговой шкале и должны быть упорядочены либо по возрастанию, либо по убыванию.

Вычисления:

1) Эмпирического распределения с теоретическим равномерным.

Для этого лучше воспользоваться таблицей 39.

Таблица 39

Разряды	f_эj	f_т	f_э_j^*	f_т^*	f_эj^*_cum	f_тj^*_cum	d

Здесь в 1 столбце даются наименования разрядов,

во 2 столбце даются эмпирические частоты по каждому разряду f_э_j, где j меняется от 1 до k,

в 3 столбце теоретическая частота, одинаковая для каждого разряда и вычисленная по формуле: f_т=n/k,

в 4 столбце находится относительная частота эмпирического распределения по каждому разряду по формуле: f_э_j^*= f_эj/n,

в 5 столбце находится относительная частота теоретического распределения по формуле: f_т^*= f_т/n,

в 6 столбце найдем относительную накопленную частоту эмпирического распределения по каждому разряду по формуле: f_э_j^*_cum= f_э(_j_-1)^*_cum+ f_э_j^*,

в 7 столбце найдем относительную накопленную частоту теоретического распределения по каждому разряду по формуле: f_т_j^*_cum= f_т(_j_-1)^*_cum+ f_т_j^*,

в 8 столбце найдем разность между 6 и 7 столбцом по модулю по формуле:

d=| f_э_j^*_cum - f_т_j^*_cum |

Далее определим, в каком разряде наибольшее значение разности, и сравним его с критическим, определенным по таблице 6 приложения 2 для данного n.

Если d_max>d_0,01, то эмпирическое распределение отличается от теоретического, если d_max £ d_0,05, то эмпирическое распределение не отличается от теоретического, если d_0,05<d_max £ d_0,01, то отличие эмпирического распределения от теоретического значимо на 5% уровне.

Пример. С учащимися 3-х классов проводилось исследование уровня притязаний. Предлагалось 12 мыслительных задач (матрицы Равена) разной степени сложности (номер соответствовал степени сложности). Можно ли утверждать, что в этом возрасте первый выбор равномерно распределяется по всем номерам задач.

Решение: n=39 это больше 5. Разрядные интервалы представлены количественно и упорядочены по возрастанию, следовательно, можно применять кр. λ.

Таблица 40

Количество учащихся, выбравших данный номер задания и расчет критерия l

№ задач	f_эj	f_т	f_э_j^*	f_т^*	f_э_j^*_cum	f_тj^*_cum	d
		3.25 3.25 3.25 3.25 3.25 3.25 3.25 3.25 3.25 3.25 3.25 3.25	0.1282 0.1026 0.1282 0.1795 0.282 0.0513 0.0513 0.0769	0.0833 0.0833 0.0834 0.0833 0.0833 0.0834 0.0833 0.0833 0.0834 0.0833 0.0833 0.0834	0.1282 0.2308 0.359 0.5385 0.8205 0.8205 0.8718 0.9231 0.9231	0.0833 0.1666 0.25 0.3333 0.4166 0.5 0.5833 0.6666 0.75 0.8333 0.9166	0.0449 0.0642 0.109 0.2052 0.4039 0.3205 0.2885 0.2565 0.1731 0.1667 0.0834

Сформулируем экспериментальную гипотезу: распределение первого выбора в 3 классе всех степеней сложности задач является равномерным.

Найдем эмпирическое значение критерия по таблице 40, где f_т=39/12=3,33. d_max=0.4039 Для n=39 определяем по таблице 6 приложения 2. d_0,01=0.2574, d_0,05=0.2147

d_max> d_0,01 Þ распределение не является равномерным.

Ответ: В 3 классе учащиеся неравномерно при первом выборе избирают разной сложности номера задач.

2) При сравнении эмпирического распределения с эмпирическим:

Вычисления также произведем с помощью таблицы 41.

Таблица 41

Разряды	f_э1j	f_э2j	f_э1_j^*	f_э2_j^*2	f_э1j^*_cum	f_э2j^*_cum	d

Вычисления аналогичны предыдущему случаю, только вместо теоретической частоты записывается частоты второго эмпирического распределения.

После нахождения максимальной разности d_max вычисляется значение критерия по формуле: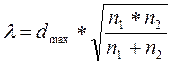

Если l>1,63, то одно эмпирическое распределение отличается от другого, если l£1,36, то первое эмпирическое распределение не отличается от второго, если 1,36<l£1,63_, то отличие двух эмпирических распределений друг от друга значимо на 5% уровне.

Пример. С учащимися 3 класса проводилось исследование на умение обобщать по тесту «пятый лишний» на вербальном и невербальном материале с одинаковым количеством заданий. За каждое правильно выполненное задание ставился балл. Результаты сгруппированных данных представлены в таблице 41. Различается ли распределение частот уровня обобщения на вербальном и невербальном материале в 3 классе?

Решение: n₁=60 и n₂=60 это больше 50. Разрядные интервалы представлены количественно и упорядочены по возрастанию, следовательно, можно применять критерий λ.

Сформулируем экспериментальную гипотезу: распределение частот уровня обобщения на вербальном и невербальном материале в 3 классе отличаются.

Найдем эмпирическое значение критерия по таблице 42.

Таблица 42

Распределение частот уровня обобщения на вербальном и невербальном материале в 3 классе и расчет критерия l

Балл	f_э1j	f_э2j	f_э1_j^*	f_э2_j^*2	f_э1_j^*_cum	f_э2j^*_cum	d
			0,05	0,02	0,05	0,02	0,03
			0,08	0,07	0,13	0,09	0,04
			0,2	0,1	0,33	0,19	0,14	d_max
			0,18	0,2	0,51	0,39	0,12
			0,17	0,28	0,68	0,67	0,01
			0,15	0,17	0,83	0,84	0,01
			0,1	0,08	0,93	0,92	0,01
			0,05	0,05	0,98	0,97	0,01
			0,02	0,03

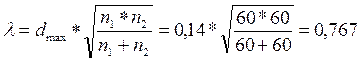
l£1,36 Þ экспериментальная гипотеза отвергается.

Ответ: распределение частот уровня обобщения на вербальном и невербальном материале в 3 классе не различается.

<8 9 101112 13 14 >

Дата добавления: 2016-01-26; просмотров: 1671;