Q-критерий Розенбаума
Непараметрический критерий, который используется для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Данный критерий является не достаточно мощным, то есть, если критерий Q не выявляет достоверных различий, это еще не означает, что их действительно нет. В этом случае стоит применять критерий U-Манна-Уитни или j* Фишера.
Критерий применяется в тех случаях, когда данные представлены в порядковой, интервальной шкале или шкале отношений. Признак должен варьировать в каком-то диапазоне значений.
Ограничения критерия:
1) n1 и n2 ³11 (n1 и n2- объемы соответственно 1-й и 2-й выборок).
2) Объемы выборок должны примерно совпадать. Так,
а) если n1 и n2£50, то ú n1-n2 ê£10;
б) если 51£n1 и n2£100, то ú n1-n2ê£20;
в) если n1 и n2>100, то n1/ n2 или n1 /n2£2.
3) Диапазон разброса значений в двух выборках должны не совпадать между собой, т.е. либо max1¹max2, либо min1¹min2.
Эмпирическое значение критерия вычисляется по формуле:
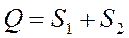
| S1 – количество значений в выборке 1-й (где значения предположительно выше), которые больше максимального значения выборки 2-й (где значения предположительно ниже); S2 – количество значений в выборке 2-й, которые меньше минимального значения выборки 1-й. |
Критические значения критерия можно определить по таблице 1 приложения 2.
Различия между выборками считаются достоверными, если Qэмп³Q0,01; незначимыми, если Qэмп< Q0,05; достоверными на 5% уровне, если Q0,05£ Qэмп <Q0,01.
Пример.С учащимися шестого класса (15 человек) и восьмого (17 человек) были проведены 8 субтестов теста структуры интеллекта Р. Амтхауера, и получен обобщенный показатель. Результаты представлены в таблице 15. Можно ли утверждать, что учащиеся восьмого класса превосходят учащихся шестого класса по обобщенному показателю теста Р. Амтхауера?
Таблица 15
Индивидуальные значения обобщенного показателя теста Р. Амтхауера учащихся шестого (n1=15) и восьмого (n2=17) классов
| 6 класс | 8 класс | ||||||
| № | Обобщенный показатель | № | Обобщенный показатель | № | Обобщенный показатель | № | Обобщенный показатель |
Решение: Данные представлены в интервальной шкале,
n1=15 и n2=17 это >11; ún1 - n2ï=2< 10;
max1=94 ¹ max2=107.
Следовательно, для решения данной задачи мы имеем право применять критерий Q.
Для вычисления необходимо упорядочить данные по убыванию. При этом значения выборки, где данные предположительно, выше записываются в 1 ряд, а где ниже, - соответственно во 2-й ряд. Так, в нашем случае 1 ряд – значения учащихся 8 класса, 2 ряд – 6 класса (таблица 16).
Сформулируем экспериментальную гипотезу: учащиеся 8-го класса превосходят учащихся 6-го класса по обобщенному показателю теста Р. Амтхауера.
Таблица 16
Упорядоченные по убыванию обобщенного
показателя теста Р. Амтхаера индивидуальные
значения учащихся 8 и 6 классов
| 1 ряд – учащиеся 8 класса | 2 ряд – учащиеся 6 класса |
| S1=4 | |
| 71 71 | |
| 69 69 | |
| S2=7 | |
| 54 54 | |
Определим максимальное значение в ряду 2-м и подсчитаем количество значений в ряду 1-м, лежащих выше этого значения: S1=4.
Определим минимальное значение в ряду 1 и подсчитаем количество значений в ряду 2, лежащих ниже этого значения: S2=7. Qэмп= 4+7= 11. По таблице 1 приложения 2 определим критические значения для n1=15 и n2=17: Q0,01=9, Q0,05=7. Qэмп>Q0,01 Þ экспериментальная гипотеза подтверждается.
Ответ: Учащиеся 8-го класса достоверно превосходят учащихся 6 класса по обобщенному показателю теста Р. Амтхауера.
Дата добавления: 2016-01-26; просмотров: 4447;
