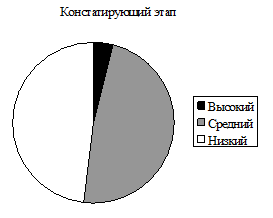
Круговая диаграмма.
Наиболее эффективно применение данного вида графика для случая, когда необходимо представлять результаты одной или двух выборок. Самое важное условие состоит в том, что в выборке, представленные категории (например, уровни, полюса, выраженность и не выраженность параметра) можно было бы представить в виде процентной доли.
Пример. С детьми 5 лет проводилась методика «Классификация геометрических фигур» до и после коррекционной программы. Результаты представлены в таблице 11.
Таблица 11
Результаты исследования классификации
геометрических фигур
| Этап Уровень | Констатирующий этап | Контрольный этап | ||
| f | % | f | % | |
| Высокий | ||||
| Средний | ||||
| Низкий |
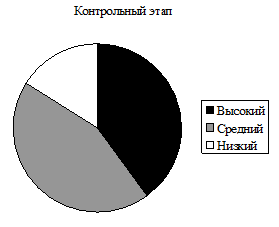
Представим эти данные в виде круговой диаграммы.
| 
|
Рис. 9. Процентное соотношение уровней классификации геометрических фигур детьми 5 лет на констатирующем и контрольном этапе.
Меры измерения
1. К мерам центральной тенденции относятся: мода, медиана и среднее арифметическое значение.
Мода – это такое значение в множестве наблюдений, которое встречается наиболее часто. Обозначается Мо
Совокупность значений может иметь одну моду (унимодальная выборка).
Примеры:
1) Совокупность значений
5, 6, 6, 8, 9, 11, 11, 11, 11, 12, 15, 15, 16 имеет Мо=11;
2) В случае, когда два соседних значения имеют одинаковую наибольшую частоту, то мода есть среднее арифметическое этих значений. Так совокупность значений 2, 2, 4, 5, 6, 6, 6, 8, 8, 8, 10, 11 имеет Мо=(6+8)/2=7.
Совокупность значений может иметь две моды (бимодальная выборка), в случае, когда два несмежных значения в выборке имеют наибольшую одинаковую частоту. Например, совокупность значений 3, 4, 4, 4, 5, 8, 9, 9, 9, 11 имеет Мо1=4 и Мо2=9.
Совокупность значений может и не иметь моды, в случае, когда все значения в группе встречаются одинаково часто (или достаточно большое количество значений имеют наибольшую одинаковую частоту).
Медиана– представляет собой 50-й процентиль в группе данных. Это значение, которое делит упорядоченное множество пополам. Обозначается Мd.
Вычисление лучше выполнять не на сгруппированных данных. Если данные определены с точностью до десятой доли (сотой и так далее), то значения лучше умножить на 10 (100 и так далее), а результат потом поделить на 10 (100 и так далее). Вычисление выполняется по тем же правилам, что и вычисление любой другой процентили (см. стр.9-10).
Среднее арифметическое значение – это сумма всех значений выборки, поделенная на количество этих значений.
Обозначается Х и вычисляется по формуле:
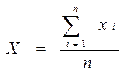
| хi- i-е значение выборки; i – порядковый номер значения в выборке; n – объем выборки. |
Например, найдем среднее арифметическое значение для данных, представленных в таблице 1. Выпишем их в упорядоченном виде:
6, 7, 7, 7, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 12, 12, 12, 14
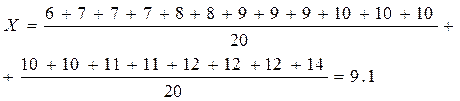
Можно формулу преобразовать для случая, когда значения повторяются.
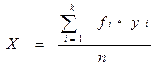
| yi – i-я варианта выборки, fi – частота i-й варианты, k – количество вариант. |
Так, для нашего случая мы получаем:
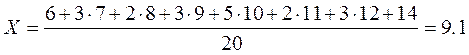
2.К мерам изменчивости относятся размах, дисперсия, среднее квадратическое отклонение, асимметрия, эксцесс.
Размах– это расстояние на числовой шкале, в пределах которого изменяются оценки. Обозначается R и вычисляется по формуле:
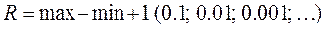
| max – максимальное значение; min – минимальное значение; |
прибавляется 1 или 0.1, или 0.01 и так далее в зависимости от того, с какой точностью определено значение.
Например, в совокупности значений
7, 9, 3, 6, 6, 2, 5 – R=9-2+1=8;
в совокупности значений
4.3, 2, 5.1, 6.2, 8.1, 5, 3.8 – R=8.1-2+0.1=6.2
Дисперсия– мера разброса данных вокруг среднего арифметического значения. Обозначается S2x и вычисляется по формуле:
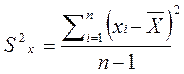 или
или 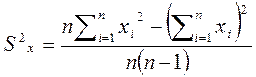 .
.
Первая формула удобна, когда вычислено среднее арифметическое значение, а вторая - когда нет необходимости вычислять это значение.
Среднее квадратическое отклонение (стандартное отклонение)– данная мера тесно связана с дисперсией, так как является квадратным корнем из нее. Обозначается s и вычисляется по формуле:
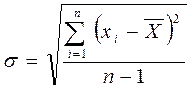 или
или 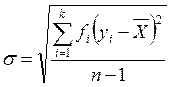
Вторая формула используется в тех случаях, когда многие значения повторяются.
Распределение на уровни. На основании вычисления среднего арифметического значения и среднего квадратического отклонения можно значения выборки распределить на уровни: высокий (В), выше среднего (ВС), средний (С), ниже среднего (НС) и низкий (Н). Так, к высокому уровню относятся все значения, которые больше или равны Х+s т.е.
В: xi³X+s;
ВС: X+0,5s<xi<X+s;
C: X-0,5s£xi£X+0,5s;
НС: X-s<xi<X-0,5s;
Н: xi£X-s.
Так, например, для данных
2, 4, 8, 3, 5, 6, 2, 5, 5, 7, 5, 3, 1, 4, 3, 3, 4, 3, 5, 1, 6, 4, 2, 5
X=4, s=1,8 (n=24), тогда
В: xi³5,8 это xi равные 6, 7, 8 (nв=4 – 16,7%);
ВС: 4,9<xi<5,8 это xi равные 5 (nвс=6 – 25%);
C: 3,1£xi£4,9 это xi равные 4 (nс=4 – 16,7%);
НС: 2,2<xi<3,1 это xi равные 3 (nнс=5 – 20,8%);
Н: xi£2,2 это xi равные 1, 2 (nн=5 – 20,8%).
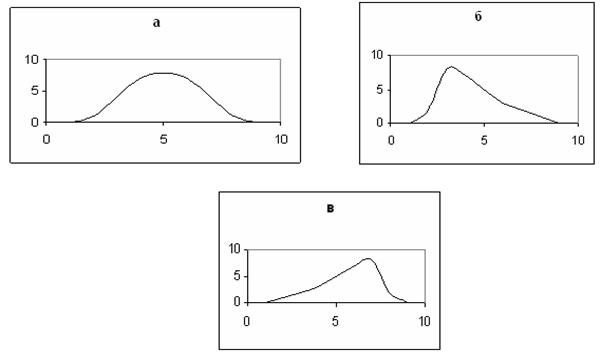
Рис. 7. Симметричный и асимметричные распределения.
Асимметрия– мера, показывающая степень и направление асимметричности графика. Обозначается А и находится по формуле:
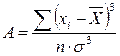 .
.
Для симметричных распределений А=0 (рис.7 а); при левосторонней асимметрии А<0 (рис.7 б) – в распределении чаще встречаются более низкие значения признака; при правосторонней асимметрии А>0 (рис.7 в) – более высокие.
Эксцесс– греческое слово, обозначающее свойство остроконечности кривой. Обозначается Е и находится по формуле:
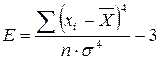 .
.
В тех случаях, когда какие-либо причины способствуют преимущественному проявлению средних или близких к средним значений, образуется распределение с Е>0 (рис.8 а). Если же в распределение преобладают крайние значения, причем одновременно и более низкие и более высокие, то такое распределение характеризуется Е<0 (рис 8 б). В распределениях с нормальной выпуклостью Е=0 (рис. 8, а и б, серая линия).
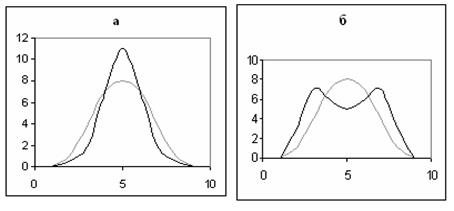
Рис. 8. Распределения с разным эксцессом.
3. Нормальное распределение – это график уравнения:
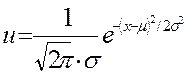
| u – высота кривой прямо над всяким заданным значением Х на графике распределения частот; m - среднее арифметическое значение; s - среднее квадратическое отклонение. |
График данного уравнения является симметричным и средневершинным.
Приведем пример графика с m=0 и s=1 (рис. 9).
Нормальная кривая – это изобретение математики, довольно хорошо описывающая полигон частот измерений нескольких различных переменных. В практике же получение такое кривой нереально. Чаще всего в ходе исследования мы получаем лишь приближенное к нормальному распределение. Существуют способы проверки распределения на нормальность. Приведем один из них.
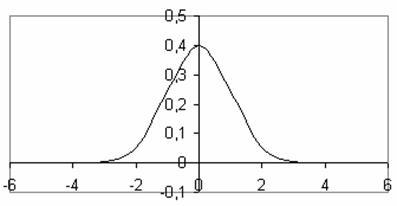
Рис. 9. График нормального распределения.
Для этого необходимо подсчитать асимметрию и эксцесс, а также их ошибки репрезентативности (ma me) по формулам:
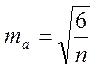 и
и 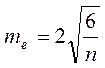 .
.
Если отношение асимметрии и эксцесса к своим ошибкам репрезентативности меньше трех, то данное распределение не отличается от нормального, т.е. должны выполняться одновременно следующие условия:
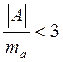 и
и 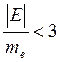 .
.
Основные понятия теории вероятностей
Событием называется всякий факт, который в результате опыта может произойти или не произойти. Например, опыт – решение тестовой задачи; события: А1 – задача решена; А2 – задача не решена.
Вероятностью события называется численная мера степени объективной возможности этого события.
Вероятность события А обозначается Р(А).
Достоверным называется событие U, которое в результате опыта непременно должно произойти:
Р(U)=1.
Например, в некоторой группе испытуемых с предложенной тестовой задачей справляются все ее члены, тогда вероятность события «задача решена» в данной группе равна 1.
Невозможным называется событие V, которое в результате опыта не может произойти:
P(V)=0.
В предыдущем примере вероятность события «задача не решена» равна 0.
Вероятность любого события А заключена между нулем и единицей:
0£Р(А)£1.
Полной группой событий называется несколько таких событий, из которых в результате опыта непременно должно произойти хотя бы одно из них.
Например, полную группу образуют события: «появление герба» и «появление цифры» в опыте бросание монеты, а неполную группу событий «появление карты червонной масти» и «появление карты бубновой масти» в опыте вынимания карты из колоды.
Несколько событий в данном опыте называются несовместимыми, если два из них не могут появиться вместе.
Например, несовместимыми событиями являются «появление герба» и «появление цифры» в опыте бросания монеты. И совместимыми могут быть события «появление герба на первой монете» и «появление цифры на второй монете» при опыте бросания двух монет.
Несколько событий в данном опыте называются равновозможными, если по условиям симметрии опыта нет оснований считать какое-либо из них более возможным, чем любое другое.
Например, равновозможными событиями являются события «появление герба» и «появление цифры» в опыте бросания монеты, но являются не равновозможными «появление герба» и «появление цифры» в опыте бросания погнутой монеты.
Если несколько событий образуют полную группу, несовместимы и равновозможны, то они называются случаями.
Случай называется благоприятным событию, если появление этого случая влечет за собой появление события.
Если результат опыта сводится к схеме случаев, то вероятность события вычисляется по формуле:
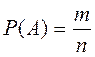 , ,
| n – общее число случаев, m – число случаев, благоприятных событию А. |
Например, опыт – постановка цвета из 8 предложенных на первую позицию (по тесту Люшера); событие А – красный цвет испытуемый поставил на 1 позицию.
В этом случае n=8, m=1.
Следовательно, P(A)=0,125.
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А и В.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и В.
Теорема сложения вероятностей:
Вероятность суммы двух несовместимых событий равна сумме вероятности этих событий:
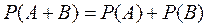 .
.
Например, опыт – постановка цвета из 8 предложенных на первую позицию (по тесту Люшера); событие А – красный цвет испытуемый поставил на 1-ю позицию и событие В – синий цвет испытуемый поставил на 1-ю позицию.
Вероятность того, что хотя бы одно из этих событий произойдет, будет вычислена по данной формуле, так как эти события несовместимы. Следовательно:
Р(А+В)=0,125+0,125=0,25.
В случае, когда события А и В совместимы, вероятность их суммы находится по формуле:
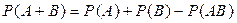 .
.
Условной вероятностью события А при наличии В называется вероятность события А, вычисленная при условии, что событие В произошло. Эта вероятность обозначается Р(А|В).
События А и В называют независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
Р(А|В)=Р(А); Р(В|А)=Р(В).
Теорема умножения вероятностей:
Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого:
P(AB)=P(A)P(B|A), или P(AB)=P(B)P(A|B).
Для независимых событий А и В
P(AB)=P(A)P(B).
Например, опыт – постановка двух цветов, из 8 предложенных, соответственно на первую и вторую позицию (по тесту Люшера); событие А – красный цвет испытуемый поставил на 1-ю позицию и событие В – синий цвет испытуемый поставил на 2 –ю позицию.
Р(А)=1/8=0,125; P(B)=1/7=0,143, т.к. n=7, потому что один цвет уже выбран и общее количество случаев сокращается на 1. Следовательно, Р(АВ)=0,125×0,143= 0,017875.
Дата добавления: 2016-01-26; просмотров: 1425;