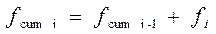Табулирование и представление данных
1. В таблице 1 приводятся результаты выполнения первого субтеста теста структуры интеллекта Р. Амтхауера в 6 классе.
Таблица 1
Результаты субтеста «логический отбор» учеников
6 класса (20 человек)
| № | Ученик | Оценка | № | Ученик | Оценка |
| Надежда Б. | Сергей К. | ||||
| Борис Б. | Дмитрий М. | ||||
| Руслан Б. | Альберт Р. | ||||
| Ольга Б. | Айгуль Р. | ||||
| Татьяна В. | Оксана С. | ||||
| Андрей В. | Инна Ш. | ||||
| Регина Д. | Михаил Ш. | ||||
| Елена Ж. | Максим Ш. | ||||
| Тамара Ж. | Алина Ю. | ||||
| Роберт И. | Павел Я. |
Упорядочим данные. Для этого выпишем все оценки от минимального к максимальному, либо от максимального к минимальному:
6, 7, 7, 7, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 12, 12, 12, 14
Многие оценки в данном списке (выборка данных) повторяются, поэтому выпишем их по одному разу и назовем вариантами. Таким образом, мы классифицируем оценки по распределению частот. Подсчитаем, сколько раз каждая варианта в выборке встречается (подсчитаем абсолютную частоту f). Выписав все варианты в упорядоченном виде и их частоты, мы табулируем данные (таблица 2).
Относительная частота обозначается f* и вычисляется по формуле:
| где n- объем выборки (количество оценок в выборке). |
Накопленная частота (или кумулятивная) обозначается fcum и вычисляется по формуле:
| где i – порядковый номер варианты; fi – абсолютная частота данной варианты; fcumi-1 – накопленная частота на предыдущей варианте. |
Считается, что fcum1=f1. fcum можно определить и по формуле:

Таблица 2
Протабулированные данные субтеста «логический отбор» из таблицы 1, подсчет относительной и накопленной частот
| Варианта | ||||||||
| f | ||||||||
| f* | 0,05 | 0,15 | 0,10 | 0,15 | 0,25 | 0,10 | 0,15 | 0,05 |
| fcum |
2. Процедура ранжирования:
1) Меньшей варианте начисляется меньший ранг, так минимальной варианте приписывается ранг 1, если ее абсолютная частота равна 1.
2) Следующей варианте приписывается следующий по порядку ранг.
3) В случае, если варианта встречается несколько раз, то ей приписывается среднее значение из тех рангов, которые бы получили оценки данной варианты, если бы они не были равны.
Например, варианта 7 встречается 3 раза. Одна оценка 7 могла бы иметь ранг 2, другая – ранг 3, третья – ранг 4. Но поскольку данные оценки равны, каждая из них получает средний ранг:
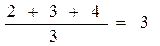
| 4) Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле: | 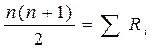
|
Таблица 3
Иллюстрация процесса ранжирования
данных (из таблицы 1)
| Варианта | ||||||||
| f | ||||||||
| Ранги | 5,5 | 15,5 | ||||||
| Вспомогательная строка | 2; 3; 4 | 5; 6 | 7; 8; 9 | 10; 11; 12; 13;14 | 15; 16 | 17; 18; 19 |
Таблица 4
Показатели оптимального темпа
детей 5-7 лет (в усл.ед)
| № исп | Оценки | № исп | Оценки | № исп | Оценки |
3.Проиллюстрируем процесс построения распределения сгруппированных частот. Группировку данных выполняют в тех случаях, когда достаточно большой объем выборки и большой диапазон разброса данных. Рассмотрим этапы группировки на примере. С помощью теппинг-теста у детей 5-7 лет (30 человек) определялся оптимальный темп в условных единицах. Результаты представлены в табл.4.
1) Определим размах по формуле:
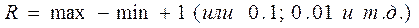
Если данные определены с точностью до целого, то прибавляется 1.
Если данные определены с точностью до десятой (например, 8,5; 7,3), то прибавляется 0.1, и так далее.
Максимальное значение в таблице 4 равняется 49, минимальное – 10. R=49-10+1=40.
2) Определим количество разрядных интервалов. Это число должно быть меньше n (объема выборки) и быть делителем размаха. Случай, когда размах простое число, рассмотрим ниже. В остальном выбор довольно произвольный. Дж. Гласс и Дж. Стенли предлагают выбирать от 12 до 15 интервалов.
В нашем случае 40 делится нацело: на 2, 4, 5, 8, 10, 20. Выберем, например 5 разрядных интервалов, т.е. а=5.
3) Определим границы интервалов.
1-й интервал: от min до min+R/a-1 (0,1; 0,01 и так далее).
2-й интервал: от min+R/a до min+2R/a-1.
i-й интервал: min +(i-1)R/a до min+iR/a-1.
Так, 1-ый интервал нижняя граница 10 – верхняя 10+40/5-1=17
2-ый инт. нижняя граница 10+(2-1)40/5=18 – верхняя 10+2*40/5-1=25
3-ый инт. нижняя граница 10+(3-1)40/5=26 – верхняя 10+3*40/5-1=33
4-ый инт. нижняя граница 10+(4-1)40/5=34 – верхняя 10+4*40/5-1=41
5-ый инт. нижняя граница 10+(5-1)40/5=42 – верхняя 10+5*40/5-1=49
Можно увидеть, что верхняя граница последнего интервала равна максимальному значению, а нижняя граница i-го интервала на 1 больше верхней границы (i-1) интервала (предыдущего).
4) Подсчитаем, сколько значений попадает в каждый разрядный интервал (табл.5)
Таблица 5
Табулирование оценок таблицы 4
| Разрядные интервалы | Подсчет количества оценок в данном интервале | f |
| 42-49 | I | |
| 34-41 | III | |
| 26-33 | IIIIIIIIIII | |
| 18-25 | IIIIIIIII | |
| 10-17 | IIIIII |
В случае, когда размах – простое число (делится только на 1 и на самого себя), например 31 (min=11, max=41), необходимо взять рядом стоящее число. Если берем меньшее (например, 30), то последний интервал будет на одно значение больше, если берем большее (например, 32), то последний интервал будет на одно значение меньше. Так, для R=31, будем считать R=30, тогда выберем а=3, и получим 1-й интервал 11–20; 2-й – 21-30; 3-й 31–41. Если будем считать R=32, тогда выберем а=4 и получим 1-й интервал 11–18; 2-й – 19–26; 3-й –27–34; 4-й – 35 –41.
4. Определение процентилей.
1-й случай. Когда интервал оценок – единица, т.е. данные не сгруппированны (данные таблицы 2). Вычислим, например, 40-й процентиль.
Вычисления выполняются за 5 шагов (табл.6).
Таблица 6
Определение P40, в распределении частот,
когда интервал оценок – единица
| Варианты | f | fcum | Вычисления |
| Шаг 1. Найти 40% от n, 0,40·20=8 Шаг 2. Найти фактическую нижнюю границу разряда оценок, содержащего fcum=8. L=8,5. Шаг 3. Вычесть накопленную к L частоту из 8 8-6=2 Шаг 4. Разделить результат 3-го шага на f верхней границы выбранного интервала. 2/3=0,66 Шаг 5. Прибавить результат 4-го шага к L P40=8,5+0,66=9,16 | |||
2-й случай. Когда интервал оценок больше единицы, т.е. данные сгруппированы (данные таблицы 5). Вычислим, например, 75-й процентиль.
Вычисления выполняются за 6 шагов (табл.7).
Таблица 7
Определение P75 по сгруппированным данным
| Разрядные интервалы | f | fcum | Вычисления |
| 42-49 | Шаг 1. Найти 75% от n, 0,40·20=22,5 Шаг 2. Найти фактическую нижнюю границу разряда оценок, содержащего fcum=22,5 L=25,5. Шаг 3. Вычесть накопленную к L частоту из 22,5. 22,5-15=7,5 | ||
| 34-41 | |||
| 26-33 | |||
| 18-25 | |||
| 10-17 | |||
| Шаг 4. Разделить результат 3-го шага на f верхней границы выбранного интервала. 7,5/11=0,68 Шаг 5. Умножить результат 4-го шага на ширину разряда оценок R/a. 0,68·8=5,44 Шаг 6. Прибавить результат 5-го шага к L. P75=25,5+5,44=30,94 |
Дата добавления: 2016-01-26; просмотров: 1260;