Напряжения в ремне и их круговая эпюра
1) напряжение от окружного усилия:
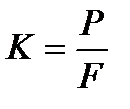
Для плоских ремней площадь сечения ремня
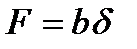
где b - ширина, d - толщина ремня.
Для клиновых ремней F определяется по таблицам ГОСТа.
2) напряжение от предварительного натяжения ремня:
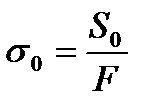
3) напряжение от усилий натяжения ремня:
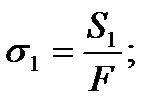

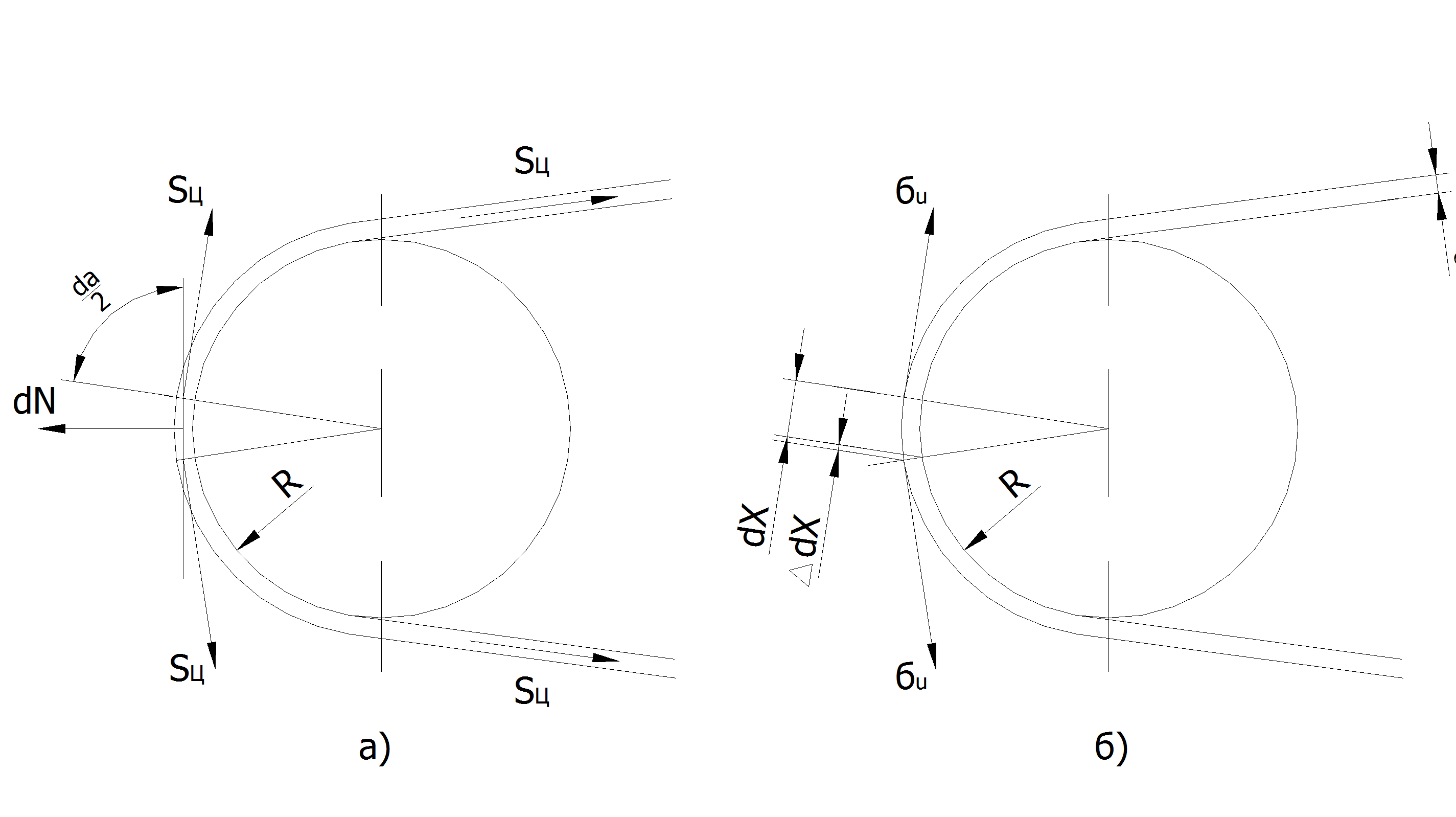
Рис. 56
4) напряжение от действия центробежных сил: Рассматривая сумму проекций сил на горизонтальную ось (рис.56 а), получим:

Синус элементарного угла 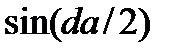 можно принять равным углу в радианах
можно принять равным углу в радианах 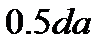 ; тогда центробежная сила элементарного участка ремня, введенного дугой
; тогда центробежная сила элементарного участка ремня, введенного дугой 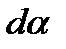 :
:
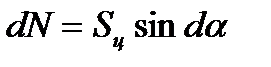 (1)
(1)
с другой стороны, элементарная центробежная сила:
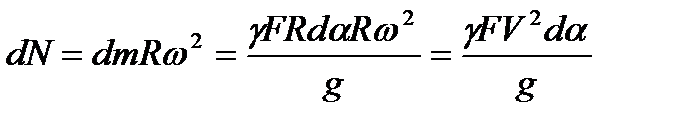 (2)
(2)
Здесь: dm - элементарная масса выделенного участка ремня;
R - радиус шкива;
w - угловая скорость вращения шкива;
g - удельный вес материала ремня;
V - окружная скорость ремня;
g - ускорение силы тяжести.
Приравнивая уравнение (1) и (2) и уравнивая размерности, получим натяжение ремня от действия центробежной силы:
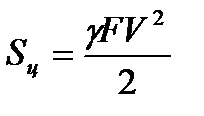
Напряжение в ремне от действия центробежной силы:
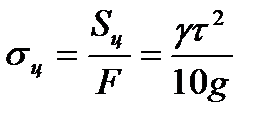
Следует заметить, что напряжение пропорционально квадрату окружной скорости; при малых скоростях оно невелико, при больших - резко возрастает.
5) напряжение от изгиба ремня:
Рассматривая подобие фигур (рис. 56 б), можно написать:
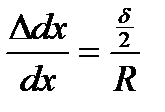 ;
; 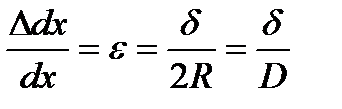
По закону Гука 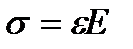 ;
; 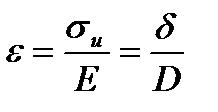 , отсюда
, отсюда
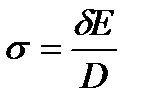
Напряжение изгиба пропорционально толщине ремня, модулю упругости и обратно пропорционально диаметру шкива. Это значит, что отношение 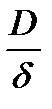 не должно быть малым (оно указывается в таблицах ГОСТа для каждого типа ремня).
не должно быть малым (оно указывается в таблицах ГОСТа для каждого типа ремня).
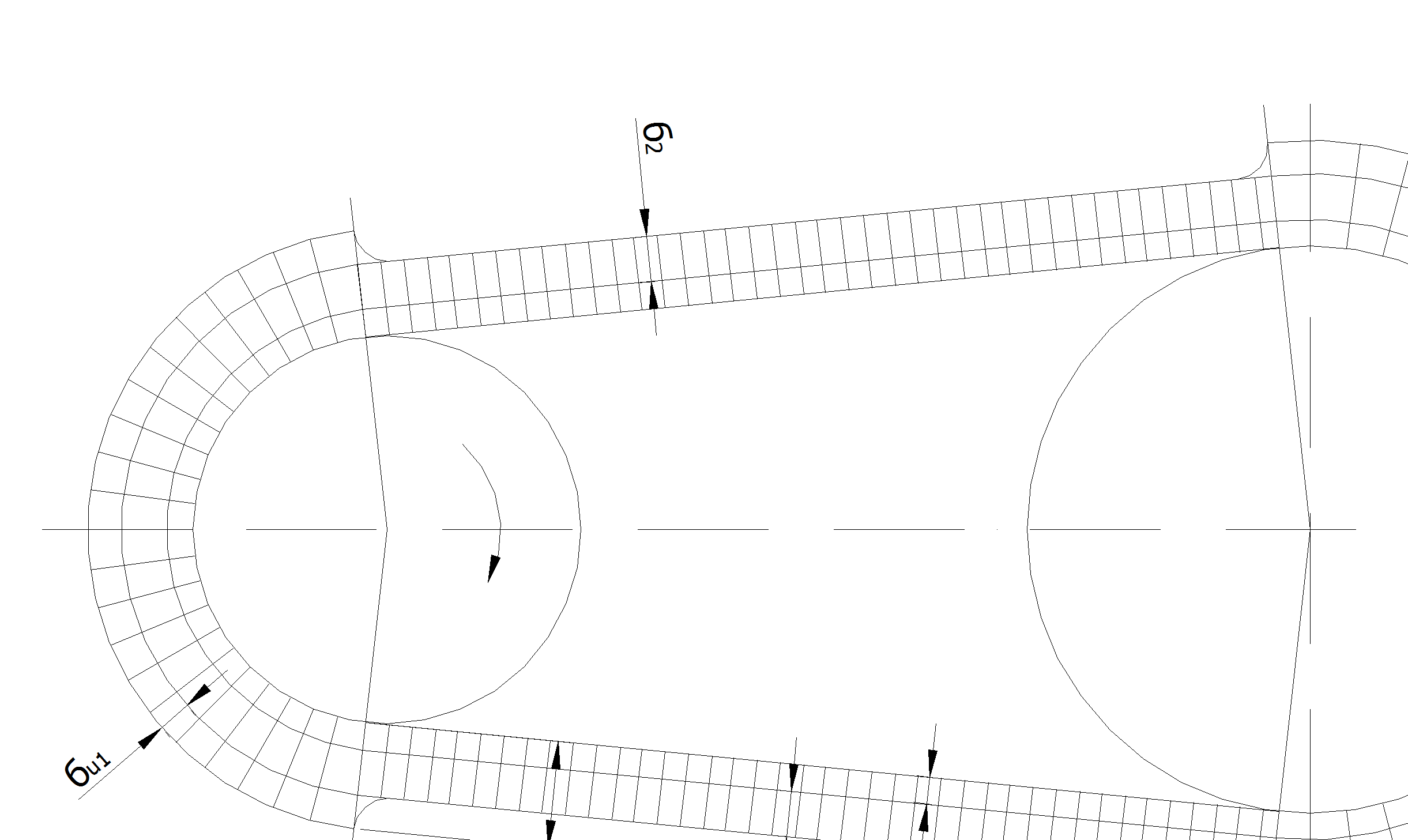
Рис. 57
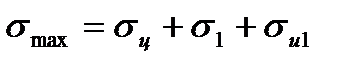
Дата добавления: 2015-11-28; просмотров: 1316;
