В любой жидкости (газе) в состоянии покоя вектор напряжения на произвольном элементе поверхности коллинеарен нормали

к поверхности и одинаков по величине для всех направлений в данной точке 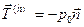. Здесь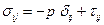 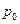— гидростатическое давление, отрицательный знак указывает на сжимающее действие напряжения при положительном значении давления. Каждое направление явля­ется главным и 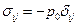. Это сферическое напряженное состояние, часто называемое гид­ростатическим сжатием. Видно, что касательные компо­ненты напряжения равны нулю в покоящейся жидкости.

При движении компоненты касательных напряжений в общем случае не равны нулю, и обычно в этом случае тензор напряжений представляют суммой двух слагаемых 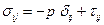, при этом 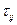называют тензором вязких напряжений, р - давле­нием. Все реальные жидкости — сжимаемые и вязкие. Однако эти свойства различны у разных жидкостей и по-разному проявляются в разных ситуациях, поэтому часто воз­можно пренебречь этими эффектами без су­щественной потери точности. Невязкая или идеальная жидкость — это жидкость, в которой 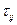тож­дественно равны нулю, даже если происходит движение. Напротив - для вязких жидкостей 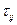нужно учитывать. Итак, для идеальной среды уравнение движения (2.2.3) называется уравнением движения Эйлера и имеет вид:

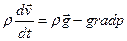(2.5.1)

Упражнение 2.1. Доказать, что ускорение в переменных Эйлера может быть представлено в виде: .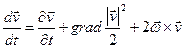

Тогда (2.5.1) можно представить в форме Громеки-Лэмба:

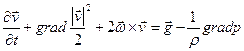(2.5.2)

Для течений идеальной жидкости дополнительным условием, позволяющим замкнуть систему из уравнений движения и неразрывности, является условие существования однозначной функции 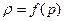, так называемое условие баротропии. Следует различать баротропные процессы и баротропные среды, для которых 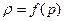является уравнением состояния.

Упражнение 2.2. Показать, что изотермическое и адиабатическое течение газа являются баротропными процессами.