Динамика сплошной среды.
Терминология. Однородной называется среда, имеющая одинаковые свойства во всех частицах. Материал будет изотропным, по отношению к некоторому свойству, если это свойство в частице оказывается одинаковым по всем направлениям. Материал является анизотропным по отношению к тем свойствам, которые зависят от направления.
В системе координат свой – чужой силы как мера механического воздействия или взаимодействия могут быть классифицированы как внешние и внутренние. Внешние силы обусловлены взаимодействием с внешними по отношению к рассматриваемой системе объектами. Внешние силы, действующие на выделенный объем сплошной среды, можно в свою очередь разделить на две категории. Силы, распределенные по всему объему сплошной среды, называются объемными или массовыми. Обычно они характеризуются своей плотностью распределения, которая определяется как предел отношения 
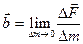 , где
, где 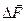 - сила, действующая на выделенную массу
- сила, действующая на выделенную массу 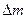 сплошной среды. Примером таких сил могут служить силы гравитации и инерции. Отметим, что массовая плотность
сплошной среды. Примером таких сил могут служить силы гравитации и инерции. Отметим, что массовая плотность 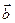 имеет размерность ускорения. Можно ввести объемную плотность сил
имеет размерность ускорения. Можно ввести объемную плотность сил 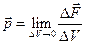 , гдеΔV объем сплошной среды. Очевидно, что если ввести плотность сплошной среды
, гдеΔV объем сплошной среды. Очевидно, что если ввести плотность сплошной среды 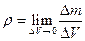 , то массовая и объемная плотность будут связаны соотношениями
, то массовая и объемная плотность будут связаны соотношениями 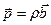 . Очень важную роль в механике сплошной среды играют поверхностные силы, распределенные по поверхности объема сплошной среды. Они также характеризуются своей поверхностной плотностью
. Очень важную роль в механике сплошной среды играют поверхностные силы, распределенные по поверхности объема сплошной среды. Они также характеризуются своей поверхностной плотностью 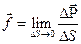 , где
, где 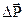
 - сила, действующая на элементΔS поверхности сплошной среды. В механике сплошной среды часто пренебрегают внутренними объемными силами, считая, что взаимодействие происходит только между частицами, близкими друг к другу, то есть действие одной части сплошной среды на другую происходит на поверхности, их разделяющей. Силы контактного взаимодействия между телами относятся к типу поверхностных сил.
- сила, действующая на элементΔS поверхности сплошной среды. В механике сплошной среды часто пренебрегают внутренними объемными силами, считая, что взаимодействие происходит только между частицами, близкими друг к другу, то есть действие одной части сплошной среды на другую происходит на поверхности, их разделяющей. Силы контактного взаимодействия между телами относятся к типу поверхностных сил.
§ 1. Принцип напряжения Коши. Вектор напряжения.
|
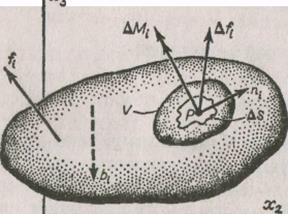
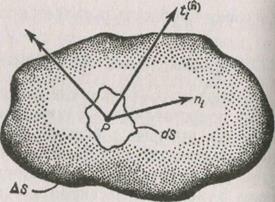
Рисунок 1.1 Рисунок 1.2
На рис 1.1 изображена область пространства, занятая материальным континуумом, на который действуют поверхностные силы 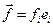 , и массовые силы
, и массовые силы 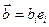 . Из-за того, что действие сил передается от одной части среды другой, материал внутри произвольного объемаV,ограниченного поверхностьюS, взаимодействует с материалом вне этого объема. Возьмем
. Из-за того, что действие сил передается от одной части среды другой, материал внутри произвольного объемаV,ограниченного поверхностьюS, взаимодействует с материалом вне этого объема. Возьмем 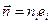 в качестве единичного вектора внешней нормали в точкеРк малой площадке поверхностиΔSи обозначим через
в качестве единичного вектора внешней нормали в точкеРк малой площадке поверхностиΔSи обозначим через 
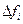 компоненты результирующей силы, действующей через площадкуΔSна материал внутриV со стороны внешней среды. Ясно, что элементарная сила
компоненты результирующей силы, действующей через площадкуΔSна материал внутриV со стороны внешней среды. Ясно, что элементарная сила 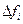 зависит от выбораΔSи от
зависит от выбораΔSи от 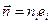 . Следует заметить, что распределение силы наΔSне обязательно однородно. В общем случае это распределение эквивалентно одной силе и моменту, приложенным в точкеРи представленным на рис. 1.1 векторами с компонентами
. Следует заметить, что распределение силы наΔSне обязательно однородно. В общем случае это распределение эквивалентно одной силе и моменту, приложенным в точкеРи представленным на рис. 1.1 векторами с компонентами 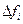 и
и 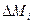 . Средняя сила, отнесенная к единице площади площадкиΔS, задается величиной
. Средняя сила, отнесенная к единице площади площадкиΔS, задается величиной 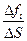 . Принцип напряжения Коши утверждает, что это отношение
. Принцип напряжения Коши утверждает, что это отношение 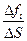 стремится к определенному пределу
стремится к определенному пределу 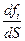 , когда ΔSстягивается в точкуР, в то время как момент силы
, когда ΔSстягивается в точкуР, в то время как момент силы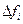 , относительно точки Р в пределе стремится к нулю. Результирующий вектор с компонентами
, относительно точки Р в пределе стремится к нулю. Результирующий вектор с компонентами 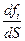 (сила, отнесенная к единице площади), называется вектором напряжения
(сила, отнесенная к единице площади), называется вектором напряжения 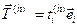 (рис.1.2). Если бы момент в точкеРпри предельном переходе не обращался в нуль, то в этой точке был бы также определен вектор момента (пары) напряжений, изображенный на рис. 1.2 стрелкой с двойным острием. В некоторых задачах приходится учитывать такие поверхностные пары, но мы их рассматривать не будем.
(рис.1.2). Если бы момент в точкеРпри предельном переходе не обращался в нуль, то в этой точке был бы также определен вектор момента (пары) напряжений, изображенный на рис. 1.2 стрелкой с двойным острием. В некоторых задачах приходится учитывать такие поверхностные пары, но мы их рассматривать не будем.
Вектор напряжения определяется следующим образом:
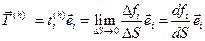 , а обозначение
, а обозначение 
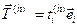 используется для того, чтобы подчеркнуть тот факт, что вектор напряжения в данной точкеР сплошной среды, очевидно, зависит от ориентации выбранного элемента поверхностиΔS, которая задается единичным вектором нормали
используется для того, чтобы подчеркнуть тот факт, что вектор напряжения в данной точкеР сплошной среды, очевидно, зависит от ориентации выбранного элемента поверхностиΔS, которая задается единичным вектором нормали 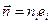 . Если взять любой иначе ориентированный элемент поверхности с другой единичной нормалью, то связанный с ним вектор напряжения в точкеРтоже будет другим. Вектор напряжения, выражающий действие через площадкуΔSв точкеРматериала, расположенного внутриV, на внешнюю среду, есть вектор
. Если взять любой иначе ориентированный элемент поверхности с другой единичной нормалью, то связанный с ним вектор напряжения в точкеРтоже будет другим. Вектор напряжения, выражающий действие через площадкуΔSв точкеРматериала, расположенного внутриV, на внешнюю среду, есть вектор 
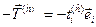 . Тогда по закону Ньютона о равенстве действия и противодействия
. Тогда по закону Ньютона о равенстве действия и противодействия 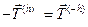 .
.
§ 2. Напряженное состояние в точке. Тензор напряжений.
Принцип напряжения Коши ставит в соответствие в произвольной частицеРсплошной среды каждому единичному вектору нормали 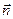 , определяющему ориентацию бесконечно малого элемента поверхности, содержащего точкуР, вектор напряжения
, определяющему ориентацию бесконечно малого элемента поверхности, содержащего точкуР, вектор напряжения 
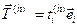 (рис.1.2), Совокупность всех возможных пар таких векторов
(рис.1.2), Совокупность всех возможных пар таких векторов 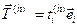 и
и 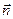 в точкеРопределяет напряженное состояние в этой точке. К счастью, для того чтобы полностью описать напряженное состояние в данной точке, нет необходимости указывать все пары векторов напряжения и нормали. Это можно сделать, задавая векторы напряжения на трех взаимно перпендикулярных площадках в точкеР, нормали к которым совпадают с векторами базиса
в точкеРопределяет напряженное состояние в этой точке. К счастью, для того чтобы полностью описать напряженное состояние в данной точке, нет необходимости указывать все пары векторов напряжения и нормали. Это можно сделать, задавая векторы напряжения на трех взаимно перпендикулярных площадках в точкеР, нормали к которым совпадают с векторами базиса 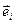 :
:

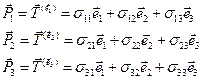 (2.2.1)
(2.2.1)
Эти векторы задаются своими компонентами 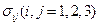 . Всего компонент девять. Покажем, что вектор напряжений на произвольной площадке выражается при помощи введенных величин
. Всего компонент девять. Покажем, что вектор напряжений на произвольной площадке выражается при помощи введенных величин 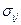 .
.
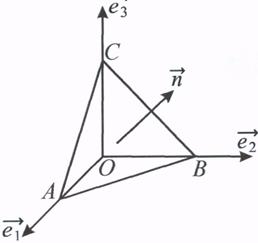 Рис. 2.3
Рис. 2.3
Рассмотрим элементарный объем в виде пирамиды - тетраэдра (рис.1.3). Внешние нормали к граням пирамиды соответственно будут: 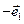 к ОВС,
к ОВС, 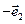 к ОВА,
к ОВА, 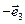 к ОСА,
к ОСА, 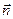 к . На грани выделенного объема сплошной среды действуют силы, равные произведению соответствующих векторов напряжений на площади. Согласно второму закону Ньютона масса выделенного элемента на ускорение его центра тяжести равна сумме всех внешних сил, то есть
к . На грани выделенного объема сплошной среды действуют силы, равные произведению соответствующих векторов напряжений на площади. Согласно второму закону Ньютона масса выделенного элемента на ускорение его центра тяжести равна сумме всех внешних сил, то есть 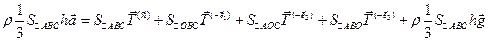 (2.2.2)
(2.2.2)
Гдеh -высота пирамиды, опущенная из вершины О;ρ-плотность сплошной среды; 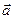
 - вектор ускорения;
- вектор ускорения; 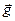 - вектор ускорения свободного падения. Заметим, что площади граней с нормалями
- вектор ускорения свободного падения. Заметим, что площади граней с нормалями 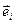 равны проекциям площади треугольника
равны проекциям площади треугольника 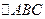 на соответствующие координатные площадки. Площадь проекции плоской фигуры равна произведению площади самой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции. Поскольку угол между плоскостями равен углу между их нормалями, получим:
на соответствующие координатные площадки. Площадь проекции плоской фигуры равна произведению площади самой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции. Поскольку угол между плоскостями равен углу между их нормалями, получим: 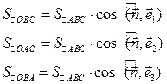 (2.2.3)
(2.2.3)
Кроме того, косинус угла между единичными векторами равен их скалярному произведению 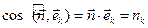
 (2.2.4)
(2.2.4)
Подставляя (2.2.1), (2.2.3), (2.2.4) в (2.2.2), после простых преобразований получим: 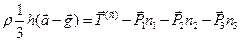 (2.2.5)
(2.2.5)
Если линейные размеры тетраэдра будут пропорционально уменьшаться, то массовые силы, малость которых на порядок выше, будут стремиться к нулю быстрее поверхностных сил. В то же время векторы средних напряжений стремятся к характерным значениям, которые присущи указанным направлениям в точкеР.Таким предельным переходом равенство (2.2.5) приводится к виду:
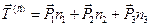 или
или 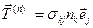 (2.2.6)
(2.2.6)
Величины 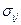 образуют компоненты тензора второго ранга - тензора напряжений. Компоненты
образуют компоненты тензора второго ранга - тензора напряжений. Компоненты 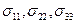 , соответствующие перпендикулярным к указанным площадкам силам, называются нормальными напряжениями. Компоненты
, соответствующие перпендикулярным к указанным площадкам силам, называются нормальными напряжениями. Компоненты 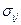
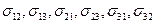 , действующие в касательных плоскостях, называются касательными напряжениями (или напряжениями сдвига). Компонента напряжения положительна, если на площадке, внешняя нормаль к которой совпадает с положительным направлением одной из осей координат, сила действует вдоль положительного направления этой оси. Компонента
, действующие в касательных плоскостях, называются касательными напряжениями (или напряжениями сдвига). Компонента напряжения положительна, если на площадке, внешняя нормаль к которой совпадает с положительным направлением одной из осей координат, сила действует вдоль положительного направления этой оси. Компонента 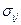 задает силу, действующую в направлении j-ой оси координат на площадку с внешней нормалью, параллельной i-ой оси координат.
задает силу, действующую в направлении j-ой оси координат на площадку с внешней нормалью, параллельной i-ой оси координат.
В тензорном виде равенство (2.2.6) можно записать в виде скалярного произведения вектора нормали 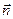 на тензор напряжений
на тензор напряжений 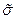 :
:
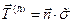 .
.
Дата добавления: 2015-12-29; просмотров: 1723;
