Приложения к разделу 2.
О теории размерности и подобия. Качественный анализ едва ли не самая важная стадия работы, когда почти без всяких вычислений получаются грубые соотношения между величинами, проясняется физическая картина явления. Один из главных элементов качественного анализа — решение задачи на упрощенных моделях, в которых отброшено все несущественное. Для качественного анализа с успехом используются методы теории размерности и подобия, а также оценки из физических соображений.
Основные положения теории размерности и подобия.
Нельзя складывать величины с разными размерностями. Не может существовать величин, например, с размерностью (метр + секунда). Как говорят, «размерность служит некоторой окраской физической величины, позволяющей отличать ее от других величин». Для того чтобы ввести понятие размерности, нужно выбрать некоторые основные физические величины и договориться в чем будем их измерять. Одной из самых распространенных систем основных единиц является система LMT , в которой в качестве основных выбираются длина (L) , масса (М) и время (Т). При этом термин «система единиц» характеризуется только выбором основных единиц и формулами, определяющими производные величины через основные, а единицы измерения основных величин здесь не принципиальны. В качестве масштабов измерения основных величин системы LMT можно указать системы СГС и международную систему единиц СИ. В первой основными приняты сантиметр, грамм-масса и секунда, во второй — метр, килограмм-масса и секунда. Сформулируем теперь основные определения и положения теории размерности:
1. Выражение единиц измерения произвольной физической величины через единицы измерения величин, принятых за основные, называется размерностью.
2. Размерность любой физической величины может быть только произведением возведенных в степень размерностей величин, принятых за основные.
3. Размерности обеих частей равенства, выражающего некоторую физическую закономерность, должны быть одинаковы.
Уже из этих утверждений следует «рецепт» решения задач методом размерности. Последовательность действий такова:
1) выбрать группу N физических величин, которые, кажутся взаимосвязанными и определяющими физику задачи (это самое трудное!);
2) выписать рядом с выбранными величинами их размерности, выраженные через К 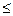 N размерностей основных величин;
N размерностей основных величин;
3) составить из выбранных величин безразмерные произведения помня, что согласно второму из приведенных утверждений, некоторые величины следует возвести в какие-то степени;
4) когда N - К = 1, безразмерное произведение будет единственным и, приравнивая его безразмерной константе, получается искомая зависимость.
Рассмотрим простой пример. Ответим с помощью анализа размерности на вопрос: «Как зависит от высоты h скорость v свободного падения тела, если начальная скорость его равна нулю?» Так как ускорение свободного падения g постоянно (не зависит от массы, плотности, упругих свойств тел и пр.), скорость может зависеть только от g и h . Итак, имеем всего три величины: v , g , h, и N = 3. В системе единиц LMT размерности этих величин следующие: [v] - L/T, [g] - L/T/T, [h] – L. В данном случае число величин с независимыми размерностями (основных величин) равно двум: L и T . Размерность M не будет входить в искомую формулу, поскольку она не входит ни в v , ни в g , ни в h. Т. е. в данном случае К = 2. Следовательно, N - К = 1. Составим произведение 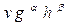 , где
, где 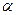 и
и 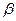 - постоянные неизвестные числа. Это произведение будет безразмерным, если потребовать обращения в нуль показателей каждой из основных величин, составляющих
- постоянные неизвестные числа. Это произведение будет безразмерным, если потребовать обращения в нуль показателей каждой из основных величин, составляющих 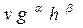 . Размерность этого произведения можно записать так:
. Размерность этого произведения можно записать так: 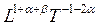 , тогда
, тогда 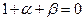 и
и 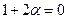 или
или 
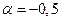 и
и 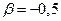 .
.
Поскольку N - К = 1, выписанная выше система уравнений имеет единственное решение; это означает, что безразмерная комбинация 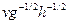 тоже единственная. Следовательно, интересующая нас зависимость имеет вид
тоже единственная. Следовательно, интересующая нас зависимость имеет вид 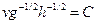 , гдеС - безразмерная постоянная, или
, гдеС - безразмерная постоянная, или 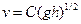 . Разумеется, обе части так полученного равенства имеют одинаковые размерности. КоэффициентСиз теории размерности найти нельзя.
. Разумеется, обе части так полученного равенства имеют одинаковые размерности. КоэффициентСиз теории размерности найти нельзя.
А что будет, если N - К > 1? Рассмотрим модель газа с плотностью молекулп .Молекулы имеют конечные размеры (пустьа— радиус или диаметр молекулы, в общем, характерный размер) и могут сталкиваться друг с другом. Оценим среднее расстояние, проходимое молекулами между двумя последовательными соударениями, которое называется длиной свободного пробега молекул (обозначим эту длину буквойl). Очевидно, что размерностьnесть 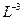 размерностиl иабудутL. Итак, основная величина в данной задаче одна — длина (К = 1), а производных величин, между которыми нужно найти связь - три ( N=3 ), т. е. N - К = 2. Комбинаций, удовлетворяющих сформулированным выше утверждениям анализа размерностей, несколько:
размерностиl иабудутL. Итак, основная величина в данной задаче одна — длина (К = 1), а производных величин, между которыми нужно найти связь - три ( N=3 ), т. е. N - К = 2. Комбинаций, удовлетворяющих сформулированным выше утверждениям анализа размерностей, несколько:
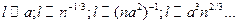
Все они допустимы. Неужели нельзя решить задачу? На помощь приходит прием, известный как дополнение Хантли, хотя сам Хантли ссылается на своих предшественников и говорит о методе векторных единиц длины. Нам не удалось решить задачу потому, что размерности всех величин, между которыми отыскивается связь, выражается только через длину. Введем несколько длин. Длину пробега любой выбранной молекулы вдоль ее траектории будем измерять в 
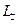 . А радиус молекул, мешающих выбранной молекуле перемещаться из-за «поперечного» расположения к траектории в
. А радиус молекул, мешающих выбранной молекуле перемещаться из-за «поперечного» расположения к траектории в 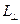 . Плотностиnможно тогда приписать размерность
. Плотностиnможно тогда приписать размерность 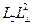 , если расположить элементарный объем-кубик так, чтобы одно ребро оказалось направлено вдоль траектории, и измерять его можно в
, если расположить элементарный объем-кубик так, чтобы одно ребро оказалось направлено вдоль траектории, и измерять его можно в 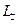 . Тогда два других окажутся перпендикулярными к траектории и их можно измерять в
. Тогда два других окажутся перпендикулярными к траектории и их можно измерять в 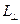 . Введя
. Введя 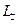 и
и 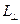 , мы увеличили число основных величин, и теперь N-К=1 (К=2). Становится ясным, что подходит только формула
, мы увеличили число основных величин, и теперь N-К=1 (К=2). Становится ясным, что подходит только формула 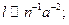 .
.
Кратко о некоторых утверждениях теории подобия.
Две или несколько физических систем называются подобными, если по заданным характеристикам одной можно получить характеристики других простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой;
Дата добавления: 2015-12-29; просмотров: 1157;
