Закон сохранения моментов количества движения.

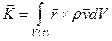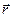Будем предполагать, что момент количества движения для сплошной среды равен моменту вектора количества движения от­носительно какой-либо точки. Так, для части континуума полный момент количества движения отно­сительно начала координат по определению равен интегралу , где - радиус-вектор элемента объемаdV. Закон сохранения моментов количества движения утверждает, что скорость измене­ния момента количества движения произвольно выбранной части континуума относительно любой точки равна главному моменту (относительно той же точки) массовых и поверхностных сил, дей­ствующих на рассматриваемую область среды. Для объемаV сплош­ной среды можно написать уравнение момента количества движе­ния в интегральной форме:

(2.4.1)

Уравнение (2.4.1) справедливо для таких сред, в которых силы вза­имодействия частиц между собой равны по величине, коллинеарны и противопо­ложны по направлению, а распределенные моменты отсутствуют. Используя методику, продемонстрированную в предыдущем параграфе, а так же то, что 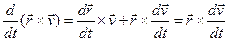, для членов (2.4.1) получим: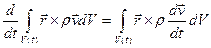

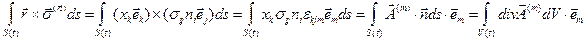
где 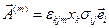, а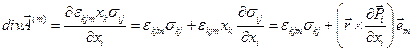

после подстановки выражения для дивергенции поверхностный интеграл примет вид 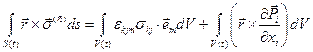и тогда (2.4.1) дает 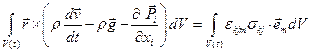, где в силу (2.3.2)

выражение слева обращается в ноль. Поэтому, следствием закона сохранения момента количества движения будут следующие равенства 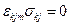(m=1,2,3). Или, если расписать подробно:

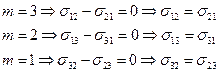(2.4.2)

Подводя итог, можно сказать следующее, закон сохранения момента количества движения для сплошной среды привел к симметрии тензора напряжений (в рамках оговоренных условий для сил и пар).