Закон сохранения количества движения.
Принцип сохранения движения впервые был сформулирован выдающимся философом и естествоиспытателем Декартом (1596-1650). Его доказательство совершенно ненаучно: «Бог незыблем, — говорит он, — а потому он должен сохранить одно и то же количество движения». Впрочем, так, как понимал его Декарт, этот принцип ложен и неразумен, поскольку им не учитывалась векторная природа импульса. Только благодаря соответствующим поправкам Гюйгенса (1629-95) измененный принцип Декарта стал одним из важнейших принципов механики — принципом сохранения проекций количества движения. Он
излагается следующим образом: сумма проекций на некоторую ось количеств движения системы (а не сумма самих количеств движения) есть величина постоянная.
Как и раньше возьмем произвольный объем сплошной среды, состоящий из одних и тех же частиц (подвижный объем). Количество движения данного (импульс) объема соответственно равно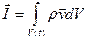 
. На выделенный объем в процессе движения действуют поверхностные и объемные силы, которые и являются причиной и мерой скорости изменения импульса. Записывается это так:
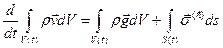(2.3.1)
Уравнение (2.3.1) является уравнением движения сплошной среды в интегральной форме, оно получено без всяких ограничений на функции, входящие в подинтегральные выражения. Ограничение одно - функции должны быть интегрируемыми. В частности, эти функции могут быть разрывными.
Потребуем теперь, чтобы все интересующие нас функции были непрерывно дифференцируемыми, тогда от уравнений в интегральной форме удается перейти к уравнениям в дифференциальной форме, более удобной для исследований. Преобразуем входящие в (2.3.1) члены по следующей методике:
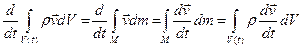
Здесь мы перешли от интегрирования по всему объему к интегрированию по массе и воспользовались тем, что массаM подвижного объема низменна.
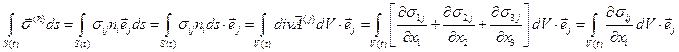Здесь мы ввели обозначение 
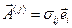и воспользовались теоремой Гаусса-Остроградского и формулой (2.2.6). Подставляя полученные значения в уравнение (2.3.1), получим 
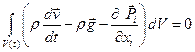. Как и в предыдущем случае, отсюда следует, что подинтегральное выражение должно быть равно нулю. То есть 
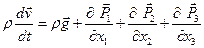(2.3.2)
Если расписать это уравнение в проекции на оси, получим три скалярных уравнения:
(2.3.3)
В результате мы получили уравнения движения произвольной сплошной среды.
Дата добавления: 2015-12-29; просмотров: 871;