Волны в идеальном сжимаемом газе. Понятие о скорости звука.
Для потенциального баротропного движения идеального газа мы получили уравнения:
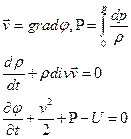(2.7.1)
Предположим, что массовыми силами можно пренебречь(U≡0). Кроме того, пусть все параметры газа изменяются вблизи некоторого равновесного состояния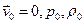 
(акустическое приближение), т.е. 
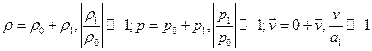, где 
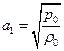- характерная скорость. Линеаризуем систему уравнений (2.7.1), выбрасывая величины, имеющие второй порядок малости, на пример:
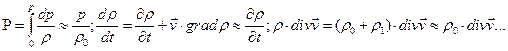и т.д. и т.п.
В результате система (2.7.1) примет вид:
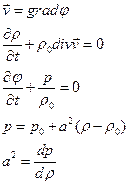(2.7.2)
Второе уравнение можно, с учетом первого и четвертого, записать в виде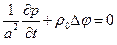 
, и если исключить из полученного уравнения и третьего уравнения (2.7.2) одну из функций: давление или потенциал, придем к волновым уравнениям:
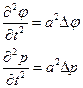(2.7.3)
Покажем, чем обусловлено название уравнения - волновое. Для этого рассмотрим одномерный случайp=p(x,t).Тогда, на пример:
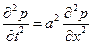(2.7.4)
Сделаем замену переменных: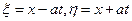 
, при этом операторы дифференцирования заменяются по формулам:
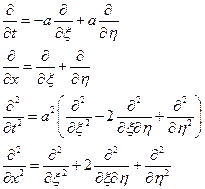(2.7.5)
Подстановка (2.7.5) в (2.7.4) приводит к уравнению: 
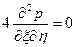, откуда 
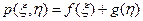или, возвращаясь к старым переменным, получим общий вид решения уравнения (2.7.4) 
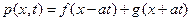. Функцияf(x-αt)описывает волну, бегущую вправо по осих, функцияg(x+αt)- волну, бегущую влево. Возмущения распространяются со скоростьюα. Поэтому 
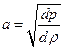называется скоростью звука в покоящемся газе.
Важно только правильно определять эту производную. Известны исторические затруднения при сравнении экспериментальной и теоретической скоростей звука Сэра Исаака Ньютона, который ошибочно полагал распространение звука изотермическим, а не адиабатическим процессом.
Упражнение 2.9. Рассмотреть сферически симметричный случай, при этом все искомые функции зависят от времени и от расстояния до центра симметрии. Показать, что основное отличие заключается в том, что в одномерном случае амплитуда волны неизменна, а в случае сферической симметрии амплитуда убывает для расходящейся и возрастает для сходящейся волны.
§ 8. Теорема живых сил. (Теорема о кинетической энергии).
Даже ошибочно сформулированный принцип сохранения движения Декарта имел большое историческое значение, так как подготовил и привел Лейбница(1646-1716) к рассмотрению живой силы. Как и Декарт и по тем же метафизическим соображениям, Лейбниц считал, что что-то должно оставаться в пространстве неизменным. Обратив внимание на то, что квадрат скорости точки является суммой квадратов составляющих, он делает вывод, что в системе материальных точек, где скорости имеют произвольные направления, надо рассматривать именно сумму произведений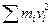 
— живую силу, а не сумму 
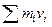, как это делал Декарт. Более того, Лейбниц вводит то, что он называет движущим действием и скрытым действием, и, согласно нему, постоянным остается движущее действие — сумма живой силы и скрытого действия. Таким образом, Лейбниц находился на пути открытия принципа сохранения энергии. Создается впечатление, что Лейбниц интуитивно предчувствовал наши современные представления. Действительно, согласно этому математику, если кажется, что движущее действие в некоторых случаях исчезает, то это связано с тем, что наблюдаемые движения преобразуются в движения молекул. Трудно яснее выразить гипотезу, которая стала основанием для механической теории тепла. Вскоре идеи Лейбница были уточнены - из них вывели теоремы живых сил. В частности, как обобщающее следствие динамических уравнений движения сплошной среды.
ПустьV – как и ранее произвольный конечный объём, движущийся с частицами сплошной среды, внутри которого все параметры - непрерывные дифференцируемые функции координат и времени, а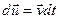 
- вектор перемещения. Умножим скалярно обе части уравнение количества движения (2.3.2) на 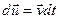и проинтегрируем по объёмуV:
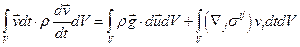(2.8.1)
Разберемся с левой частью:
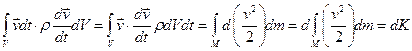
, где по определению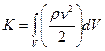 
- кинетическая энергия объёма Vсплошной среды.Первое слагаемое правой части:
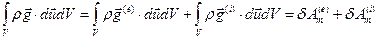, где черезА обозначены работа внешних и внутренних по отношению к объемуVмассовых сил при бесконечно малом перемещении. Заметим, что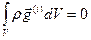 
всегда, но 
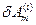может отличаться от нуля. Последний интеграл в выражении (2.8.1) запишем в виде:
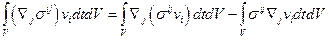(2.8.2)
Первый интеграл справа в (2.8.2) преобразуем по теореме Гаусса-Остроградского: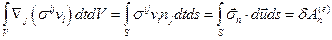 
по определению называется работой внешних поверхностных сил, действующих на поверхностьS объемаVпри бесконечно малых перемещениях точек поверхности. Для преобразования второго интеграла справа в (2.8.2) воспользуемся тождеством (1.5.1):
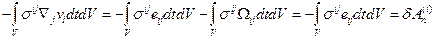, по определению называется работой внутренних поверхностных сил, действующих на поверхностьS объемаVпри бесконечно малых перемещениях точек поверхности (при этом мы воспользовались симметрией тензора напряжений и тем, что свертка симметричного и антисимметричного тензоров равна нулю).
Таким образом, из (2.8.1) получили теорему живых сил:
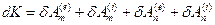(2.8.3)
Дата добавления: 2015-12-29; просмотров: 788;