Безразмерные комплексы размерных величин, представляющие собой произведения различных степеней этих величин, называются
критериями подобия. Их, как правило, обозначают буквой П;
3. П-теорема.Функциональная зависимость между характеризующими процесс размерными величинами может быть представлена в виде зависимости между составленными из них критериями подобия.
Остановимся более подробно на этой теореме, которая является основным и единственным содержательным утверждением теории размерности и подобия. Пусть интересующая нас физическая система характеризуетсяпразмерными величинами, которые будем называть определяющими и обозначать как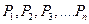 
. Если из физических соображений известно, что размерная величина 
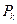является функцией остальных размерных величин, то имеет место соотношение:
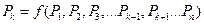
Функциональная связь между размерными величинами может быть представлена и в неявной форме, например: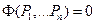 
или в форме нескольких неявных функций.
П-теорема утверждает, что выписанные выше функциональные соотношения могут быть представлены в виде:
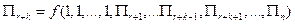
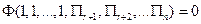
гдеr- число величин с независимыми размерностями (основных величин). Еслип – r=1, то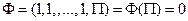 
, причем, как правило, корень получившегося уравнения по порядку величины не сильно отличается от единицы. Если жеп =rто все размерности независимы и 
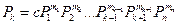, гдес- безразмерная постоянная, а показатели 
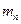легко определяются с помощью формулы размерности для 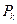. Следует подчеркнуть, что конечной целью теории размерности и подобия является определение структуры критериев подобия 
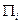либо на основе анализа размерностей, либо из уравнений процесса.
В качестве примера важности критериев подобия рассмотрим задачу об обтекании твердого тела жидкостью. Скоростьuнабегающего потока жидкости считаем постоянной (движения стационарные и не зависят от времени), жидкость - несжимаемой. В жидкости существуют силы трения, возникающие между ее соседними слоями из-за разных скоростей их движения. Такую жидкость называют вязкой и характеризуют коэффициентом динамической вязкости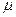 
или коэффициентом кинематической вязкости 
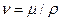. Искомой величиной в данном случае будет векторная скоростьvтечения, которая зависит от пространственных координат, т. е. от вектораr. Течение жидкости, очевидно, будет зависеть от размеров и формы движущегося в жидкости тела. Форма тела считается заданной, поэтому его геометрические свойства определяются каким-нибудь одним линейным размеромl(например, для шара или цилиндрической трубы это радиус). Таким образом, телами одинаковой формы будут называться геометрически подобные тела, т. е. такие, которые могут быть получены друг из друга изменением линейных размеров в одинаковое число раз. Итак, искомая зависимость может быть записана в виде 
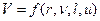, где в системе LMT 
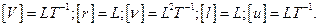Будем измерять длины в единицахl,а скорости в единицахи, т.е. введем безразмерные величиныv/uиr/l
. Из величин 
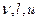, определяющих каждый тип движения жидкости, можно составить всего одну безразмерную комбинацию 
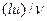, которая называется числом Рейнольдса и обозначается через Rе:
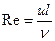
Тогда, учитывая, что число Рейнольдса является единственным безразмерным параметром, можем записать:
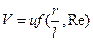
Из последнего выражения видно, что в двух разных течениях одного типа (например, обтекание шаров разного радиуса жидкостями разной вязкости) величины безразмерных скоростейV/иявляются одинаковыми функциями отr/lпри одинаковых для этих течений числах Рейнольдса. Применительно к данной задаче приведенное выше первое утверждение теории подобия звучит так: два или несколько течений называются подобными, если они могут быть получены друг из друга простым изменением масштаба координат и скоростей. Таким образом, число Рейнольдса есть критерий подобия и должно быть одинаковым в подобных движениях. Что изменится, если движение станет нестационарным? Тогда, наряду с величинами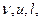 
, нужно ввести характерное для этого движения время 
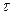(например, при колебаниях погруженного в жидкость тела определенной формы за 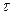можно принять период колебаний). Из четырех размерных величин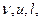 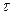можно составить уже две безразмерные величины - число Рейнольдса и число, называемое числом Струхаля:
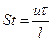
Подобие движений имеет место при равенстве в разных движениях обоих этих чисел. Детальные эксперименты специалистов по гидродинамике и биомеханике показали, что при движении любых живых организмов, реализующих «изгибный» механизм плавания, независимо от размера тела число Струхаля остается постоянным. В этом случае 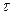- период осцилляций хвоста,и -скорость рыбы иl - размах осцилляции хвоста.
Чтобы плавание было эффективным, нужноSt ~ 0,3. В природе для любых рыб реализуется именно это значение. ЕслиSt = сопst, то скорость рыбы будет тем больше, чем большеl.Энергетически выгодно плавать так, чтобыlравнялась длине тела. Последнее возможно, когда изгибные колебания имеют длину волны, равную длине тела. Так, например, и плавает минога, которая изучена очень хорошо. Рисунок иллюстрирует, как получается число Струхаля у рыб, которые плывут за счет того, что создают бегущую волну, распространяющуюся вдоль тела с постоянной скоростью.
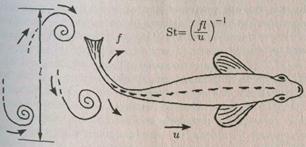
Иллюстрация образования числа Струхаля при «изгибном» плавании, когда вдоль тела рыбы с постоянной скоростью распространяется бегущая волна. Тогда волны сохраняют свойства и при изменении скорости плавания; причем, на длине рыбы укладывается одно и то же число волн (от 0,6 до 1,0). Скорость перемещения регулируется частотой осцилляции хвоста (частотой срыва вихрей). Диапазон скоростей и частот зависит от вида и размеров рыб (например, для форели частоты меняются от 3 до 25 Гц).
В чем же сила теории подобия? В том, что, изучив одно течение, мы получаем информацию и обо всех других, для которых выполняются условий подобия; в том, что, поняв, как плавает минога, можно «разобраться в механизме управления плаванием многих позвоночных от маленькой кильки до акулы». В теории размерности и подобия устанавливаются условия, которые должны соблюдаться в опытах с моделями, и выделяются характерные и удобные параметры, определяющие основные эффекты и режимы процессов. Вместе с тем сочетание соображений теории размерности и подобия с общим качественным анализом механизма физических явлений в ряде случаев может служить плодотворным теоретическим методом исследования.
Дата добавления: 2015-12-29; просмотров: 2322;