Алгоритмы вычисления суммы и произведения

При вычислении суммы или произведения ряда чисел пользуются соответствующими формулами.

ФОРМУЛА СУММЫ

S_i=S_i-1+x_i

Сумма равна предыдущей сумме плюс аргумент. Начальная сумма равна нулю. При нахождении количества аргумент равен одному.

ФОРМУЛА ПРОИЗВЕДЕНИЯ

P_i=P_i-1*x_i

Произведение равно предыдущему произведению, умноженному на аргумент. Начальное произведение всегда равно единице.

Математически данные формулы записываются так (рис. 9.14).

Если в аргументе около имени какой-нибудь величины стоит индекс счетчика, то внутри цикла необходимо поставить блок ввода этой величины.

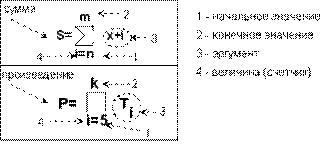
Рис. 9. 14. Формулы для вычисления суммы и произведения

В качестве примера рассмотрим блок-схемы алгоритмов для приведенных на рис. 9.14 примеров.

Вложенные циклы

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.

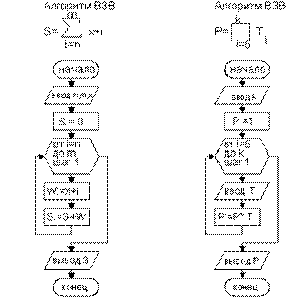
Рис. 9. 15. Блок-схемы алгоритмов вычисления суммы и произведения

При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.

Рассмотрим два примера вычисления вложенных циклов.

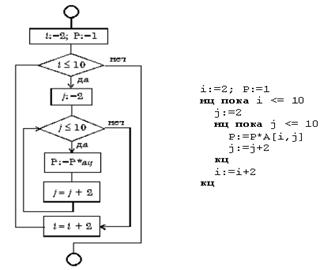
Рис. 9. 16. Вложенный цикл "до"

Вложенный цикл "до"

Пример

Вычислите произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов (рис. 9.16).

Вложенный цикл "пока"

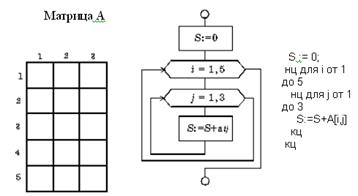
Рис. 9. 17. Вложенный цикл "пока"

Пример

Вычислите сумму элементов заданной матрицы А(5,3) – рис. 9.17.