Алгебраические свойства векторного произведения

1) ;

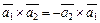2)

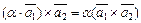
3) ;

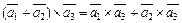4) .

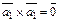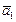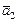Докажем свойство 1. Если векторы и коллинеарны, тогда 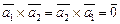, то есть 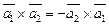. Если векторы 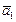и 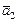не коллинеарные, то при очевидной одинаковой длине выполняется 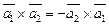, иначе обе тройки векторов 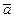, , 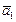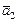и 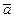, , 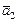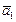были бы правыми, что невозможно в силу их противоположной ориентации.

Упражнение. Доказать свойства 2) – 4).

Выразим векторное произведение векторов 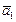и 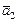через их координаты. Имеем

.

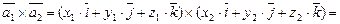
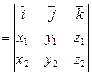При доказательстве достаточно заметить, что 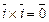, , 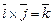, , 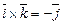, , 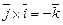, , 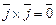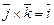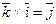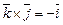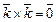. Далее раскладывая определитель по элементам 1-ой строки, получаем требуемое.

Если векторы 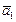и 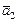коллинеарны, то их координаты пропорциональны, то есть

.

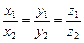Замечание. Допускается иметь в знаменателе 0, если всякую пропорцию 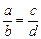понимать как .

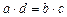Пример IV.7. Найти площадь треугольника АВС с вершинами , , .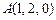

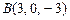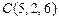Решение. Воспользуемся свойством 4) векторного произведения: площадь треугольника равна половине площади параллелограмма, построенного на векторах 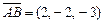и 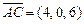. Вычислим их векторное произведение, имеем:

.

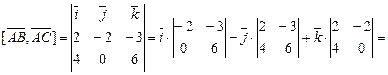
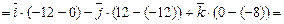
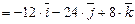Площадь треугольника ABC равна половине величины этого векторного произведения:

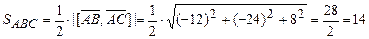кв.ед.

§ 7. Смешанное произведение векторов [4]

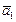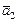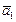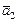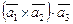Пусть даны три вектора , , . Если векторно умножить на , а затем скалярно на вектор , то получим число , называемое смешанным произведением.

Геометрически смешанное произведение векторов 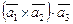равно объему параллелепипеда, построенному на этих векторах, если они образуют правую тройку, и со знаком «-» в противном случае.

Выразим смешанное произведение векторов 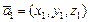, , 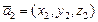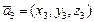через их координаты, тогда имеем

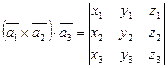. (IV.14)

Для доказательства достаточно учесть

,

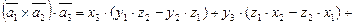
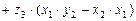а затем разложить определить по 3-й строке и обнаружить совпадение.

Теорема IV.2. Необходимым и достаточным условием компланарности трех векторов является равенство 0 их смешанного произведения.

Следствие. Смешанное произведение трех векторов, два из которых совпадают, равно 0.

Для доказательства достаточно воспользоваться условием равенства 0 смешанного произведения и воспользоваться формулой (IV.14).

Пример IV.8. Найти объём тетраэдра, вершинами которого являются точки , , , .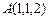

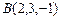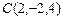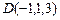Решение. Объём тетраэдра составляет шестую часть объёма параллелепипеда, построенного на векторах 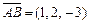, 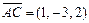и 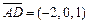. Найдем смешанное произведение этих векторов:

.

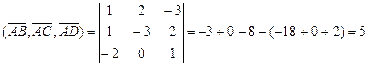Таким образом, объем тетраэдра равен

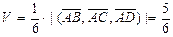куб. ед.

V. Аналитическая геометрия [4]

Аналитическая геометрия – раздел геометрии, изучающий геометрические образы алгебраическими средствами, основывающимися на методе координат.