Деление отрезка в данном отношении
Рассмотрим в пространстве вектор 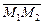 (рис. IV.7). Пусть M – внутренняя точка направленного отрезка, тогда
(рис. IV.7). Пусть M – внутренняя точка направленного отрезка, тогда 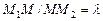 . Число l называется отношением, в котором точка M делит отрезок
. Число l называется отношением, в котором точка M делит отрезок 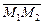 .
.
Вычислим координаты точки 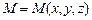 , которая делит отрезок
, которая делит отрезок 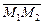 в отношении l, где
в отношении l, где 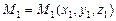 ,
, 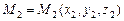 .
.
Учитывая формулы (IV.8 а) – (IV.8 в), получаем
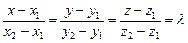 .
.
Приравнивая последовательно дроби к числу l, будем иметь
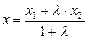 ,
, 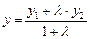 ,
, 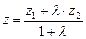 . (IV.10)
. (IV.10)
Формулы (IV.10) называются формулами деления отрезка в отношении l.
Пример IV.1. Для деления отрезка пополам, полагая 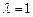 , получаем координаты точки
, получаем координаты точки 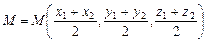 .
.
Замечание. Для положительных значений l точка M лежит между точками M1 и M2, для отрицательных – вне отрезка 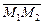 . Для
. Для 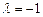 формула (IV.10) не имеет смысла.
формула (IV.10) не имеет смысла.
Упражнение. Получить формулы (IV.5), используя преобразование подобия.
Пример IV.2. Начало вектора находится в точке 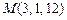 , конец в точке
, конец в точке 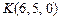 . Найти координаты вектора
. Найти координаты вектора 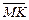 , его длину и направление.
, его длину и направление.
Решение. Для того, чтобы найти координаты вектора 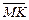 ,нужно от координат конца вычесть координаты начала вектора:
,нужно от координат конца вычесть координаты начала вектора:
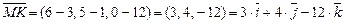 .
.
Найдем длину вектора: 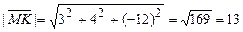 .
.
Теперь по формулам (IV.10) имеем: 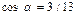 ,
, 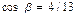 ,
, 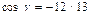 .
.
Дата добавления: 2016-01-26; просмотров: 1270;
