Линейные операции над векторами. Под линейными операциями над векторами понимают операции сложения векторов и умножение их на число.

Под линейными операциями над векторами понимают операции сложения векторов и умножение их на число.

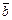Геометрическая интерпретация. Пусть и два произвольных вектора. Возьмем произвольную точку O и построим из нее вектор 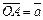. От точки A отложим вектор 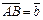. Вектор 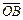, соединяющий начало первого вектора с концом второго, называется суммой векторов и : 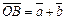(рис. IV.1).

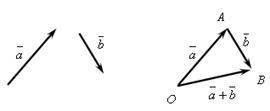
Рис. IV.1

Это правило сложения векторов называется правилом треугольника. Аналогично происходит сложение нескольких векторов (рис IV.2):

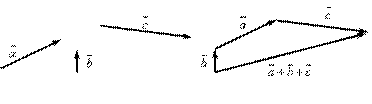
Рис. IV.2

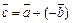Под разностью векторов и понимается вектор . На практике вектора и откладывают из одной точки, концы соединяют и вектор имеет направление «к концу вектора ».

Отметим, что в параллелограмме (рис. IV.3), построенном на векторах и , одна направленная диагональ является суммой векторов и 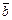, а другая - разностью.

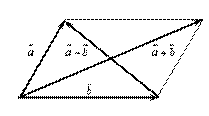
Рис. IV.3

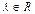Произведением вектора на скаляр (число) λ, , называется вектор 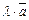, который имеет длину вектора , умноженную на λ, а направление совпадает с направлением вектора , если 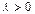, и противоположно направлению вектора , если .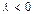

Линейные операции над векторами обладают следующими свойствами:

1) 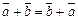;	3) ;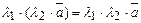
2) 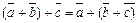;	4) ;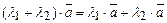
5) , .

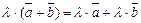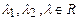Эти свойства позволяют проводить преобразования над векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.