Координатные системы

Координатные системы или системы координат – от латинских слов coordinatus – совместно, ordinatus – упорядоченный [3] (см стр. 78, [11]).

При решении различных задач, возникающих из потребностей практики, часто требуется знать характеристики положения тела в пространстве, его протяженность, взаимное расположение с другими телами и т.д.

Из соображений практической целесообразности часто требуется рассматривать тело как точку на прямой, плоскости или в пространстве, а ее движение описывать вектором. Положение такой точки в пространстве можно полностью определить ее координатами относительно любого базиса, то есть упорядоченным набором чисел.

Пусть дана направленная геометрическая прямая линия (рис. III.3).

Рис. III.3.

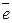Рассмотрим линейное пространство L векторов на прямой. Зафиксируем на ней начало O и единичный вектор , где 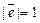. Положение любой точки M на прямой, очевидно, однозначно определяется вектором 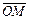. Все векторы на прямой коллинеарны, следовательно, существует число 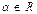, такое, что 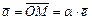. Число a называется аффинной координатой. Таким образом, каждая точка M на прямой, в самом деле, однозначно определяется аффинной координатой a. При фиксированной аффинной системе координат существует однозначное соответствие между всеми действительными числами (числовая ось) и точками прямой линии.

В одномерном пространстве мы уже можем вычислять расстояние между двумя точками 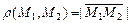, геометрически интерпретируя его как длину отрезка. В самом деле, из аксиом линейного пространства имеем , , 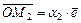тогда 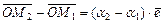, отсюда длина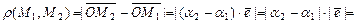

.

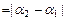Аналогично рассмотрим плоскость, на которой зафиксируем начало и неколлинеарные единичные векторы 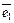, 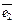с общим началом, тогда получаем аффинную систему координат (рис. III.4), в которой любой вектор 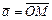однозначно определяется двумя координатами , .

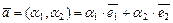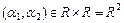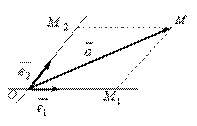
Рис. III.4

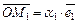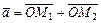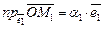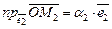Векторы , , а . Тогда M₁ и M₂ называются аффинными проекциями вектора на оси координат , . Если 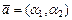, то , 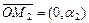. Каждый базисный вектор на своей оси образует собственную одномерную систему координат.

Задание упорядоченной пары чисел однозначно определяет точку плоскости. Следовательно, при заданной системе координат существует взаимно-однозначное соответствие между всеми упорядоченными парами вещественных чисел и точками плоскости.

Аналогично вводится аффинная система координат в пространстве с базисными векторами 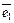, , 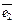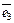. Положение любой точки M в пространстве однозначно определяется вектором 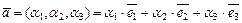, где 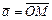, а координаты называются 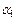– абсциссой, 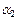– ординатой, 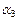– аппликатой точки M. Соответствующим образом определяются проекции на оси.

Заметим, что проекцию точки в пространстве можно задать и на координатной плоскости.

Среди аффинных координат наибольшее распространение получили декартовые координаты, характеризующиеся тем, что базисные единичные векторы взаимно ортогональны и обычно обозначаются буквами 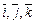. Их преимущество по сравнению с другими координатными системами только в простоте получаемых формул, отражающих измерения и взаимное расположение объектов в линейных пространствах.

Метод координат – хорошо разработанный аппарат, исследующий геометрические объекты алгебраическими и математического анализа методами. Этот метод лежит в основе аналитической геометрии – прикладной математической науки, изучающей геометрические объекты аналитическими методами.

Как уже отмечалось, линейная алгебра широко применяется в различных науках, и ее связь с аналитической геометрией вполне естественна. Можно сказать, что линейная алгебра является ее теоретической базой. В дальнейшем эта связь будет постоянно подтверждаться.