Пример III.11 (теорема Кронекера – Капелли).

Пусть имеем систему линейных алгебраических уравнений

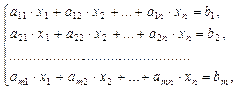(III.5)

где A – матрица коэффициентов системы, 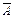- расширенная матрица коэффициентов системы

, .

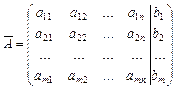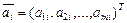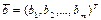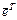Будем считать столбцы расширенной матрицы коэффициентов векторами , , где – транспонированная вектор-строка. Запишем вектор 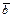как линейную комбинацию

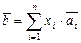, где , (III.6)

эта запись эквивалентна системе уравнений (III.5).

Теорема III.4 (Кронекера – Капелли). Система линейных алгебраических уравнений (III.5) совместна тогда и только тогда, когда ранг матрицы A равен рангу матрицы 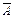, то есть .

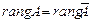Доказательство. Необходимость. Пусть система (III.5) совместна, тогда у нее существует решение: 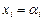, , 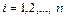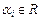. Учитывая (III.6), 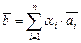, но в этом случае 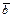есть линейная комбинация векторов 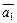, , 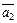…, 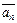. Следовательно, через множество векторов 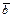, , 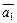, 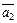…, 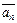можно выразить любой вектор из 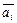. Это означает, что .

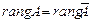Достаточность. Пусть 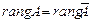. Выберем любой базис из 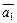, , 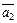…, , 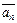тогда 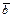линейно выражается через базис (это могут быть как все векторы 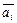, так и их часть) и тем самым, через все векторы 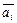, 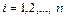. Это означает, что система уравнений совместна ▼.

Рассмотрим n-мерное линейное пространство L. Каждый вектор можно представить линейной комбинацией 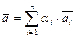, где множество 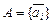, 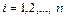состоит из базисных векторов. Перепишем линейную комбинацию в виде 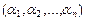и установим взаимнооднозначное соответствие между элементами и их координатами

,

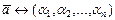где .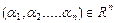

Это означает, что между n-мерным линейным векторным пространством векторов 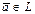над n-мерным полем действительных чисел 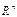установлено взаимно-однозначное соответствие.

Определение. Два линейных пространства и 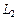над одним и тем же скалярным полем изоморфны, если между их элементами можно установить взаимнооднозначное соответствие f, так чтобы

,

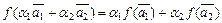то есть под изоморфизмом понимается взаимнооднозначное соответствие, сохраняющее все линейные отношения. Ясно, что изоморфные пространства имеют одинаковую размерность.

Из примера и определения изоморфизма следует, что с точки зрения изучения проблем линейности изоморфные пространства одинаковы, поэтому формально вместо n-мерного линейного пространства L над полем 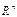можно изучать только поле .

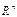Подпространства

Линейные пространства изучают не только отношения между элементами, но и прямые, плоскости и другие линейные аналоги геометрических образов.

Определение. Непустое множество M линейного пространства L называется подпространством или линейным многообразием [11], если из принадлежности 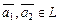следует, что ему принадлежат все линейные комбинации .

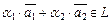Последнее означает, что с любым элементом оно содержит и элемент 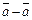, то есть нулевой элемент 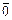.Поэтому, говоря о подпространствах (прямых, плоскостях и т.д.), следует иметь в виду, что все они содержат нуль-вектор или проходят через начало координатной системы, если таковая введена.

Следовательно, любое подпространство является пространством.

Очевидными примерами подпространства являются само пространство L и множества О, состоящее из одного элемента
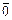{ } или начала.

Пример III.12.Выберемв трехмерном линейном пространстве три единичных взаимно перпендикулярных вектора и приведем их к общему началу (рис. III.1), которое обозначили через O.

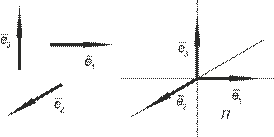
Рис. III.1

Из определения подпространства следует, что пространство 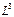есть объединение подпространств и 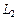с базисам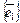и и 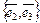соответственно. Ясно, что 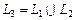и 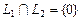, где множество 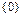содержит один элемент 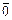– нуль-вектор. Из рисунка видно, что 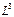является объединением плоскости P и прямой l. Приведение к общему началу позволяет ввести прямоугольную координатную систему с заданным масштабом 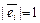и направлением.

Прямые суммы

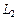Пусть и линейные пространства над одним и тем же числовым полем R. Их прямой суммой называется линейное пространство 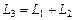, элементами которого являются всевозможные пары элементов 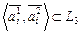, где 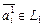, , 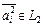а линейные операции определяются формулой

.

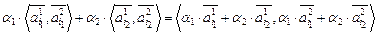Множество всех элементов вида á ,0ñ образует в 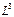подпространство, соответствие á ,0ñ® показывает, что это подпространство изоморфно , а á0, ñ – .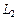

Какова связь между и 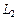, если их рассматривать как подпространства ?

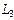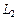Теорема III.5. Если и подпространства линейного пространства 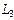, то следующие условия эквивалентны

1) ;

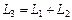2) 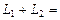Ơ, где Ơ={0} – нуль-пространство и 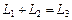(то есть и 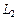дополняют друг друга);

3) любой элемент 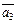из 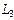можно записать как 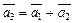, где 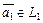, 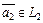(рис. III.2).

Рис. III.2

Теорема III.6. Размерность прямой суммы равна сумме размерностей ее слагаемых.

Следствие. Любое подпространство конечного линейного пространства обладает дополнением.

Пример III.13. Пусть элементы , , , 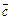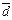принадлежат 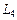, а и 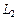подпространства такие, что , .

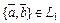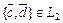Проверить равенство , если

а) , , , ;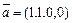

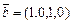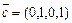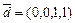б) , , , .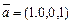

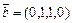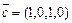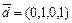Имеем 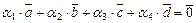или

.

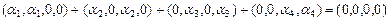По правилу сложения координат получили а) 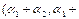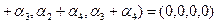. Приравнивая соответствующие координаты правой и левой частей последнего равенства, получим систему уравнений, решение которой имеет вид: 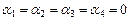, то есть элементы линейно независимые. Рассматривая пары 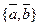, , 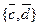получаем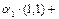 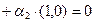Þ 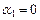, 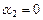. Таким образом, равенство верно.

Аналогичные вычисления для случая б) дают 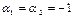, , 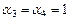то есть элементы линейно зависимые, .

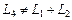Докажем теорему (о размерности пространства), используя разложение пространства в прямую сумму подпространств.

Теорема III.7. Все базисы n-мерного линейного пространства 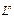состоят из n элементов.

Доказательство.Рассмотрим n-мерное линейное пространство 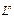, 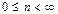. Доказательство проведем методом математической индукции.

При 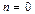число базисных векторов равно 0, что следует из определения линейной комбинации. При 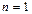число базисных элементов 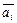равно 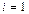. Любой другой элемент получается умножением базисного на число 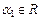, то есть 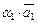, следовательно, базис одномерного линейного пространства (прямая) состоит из одного элемента.

Предположим, что n-мерное линейное пространство 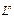состоит из n базисных элементов. Докажем, что n+1-мерное линейное пространство 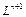состоит из (n+1) базисного элемента. В самом деле, представим (n+1)-мерное пространство 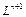в виде прямой суммы подпространств , где 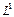– одномерное линейное пространство, что возможно в силу предыдущей теоремы. Любой элемент пространства 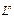получается умножением базисных элементов 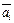на число 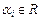, , 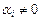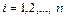. В силу свойств прямой суммы получаем, что любой базис пространства 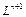состоит из n+1 элемента и число базисов в любом линейном пространстве 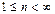бесконечно ▼.

Замечание. Между прочим, доказательство по индукции можно было начинать с 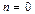, не акцентируя внимание на .

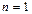Замечание. Из теоремы, в силу метода индукции, следует, что потенциально любое линейное пространство содержит столько базисных векторов, какова его размерность.

Пример III.14.Рассмотрим три единичных взаимно перпендикулярных вектора 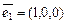, , 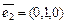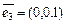. С точностью до изоморфизма возможно разложение в прямую сумму по базисным векторам для 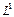любой из 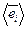, для 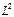– любая пара 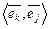, 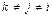. Аналогично можно составить базис бесконечномерного пространства.