C. Дистрибутивность.

7) Следует из свойств пропорциональности отрезков
(рис. III.3). В самом деле, 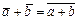. Пусть 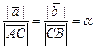, тогда

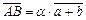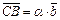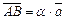, , Þ .

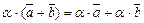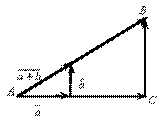
Рис. III.3

8) Следует из рис. III.2 и правил сложения векторов, если положить 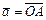, , 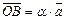, 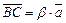тогда .

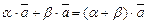Тем самым выполнение аксиом показано геометрически.

Пример III.2. Пусть R² множество всех упорядоченных пар действительных чисел и 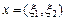, , 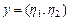где 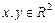. Положим по определению

1) ;

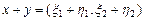2) ;

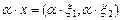3) ;

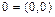4) ,

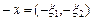где .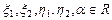

Аксиомы групп A, B, C, очевидно, выполняются, следовательно, R² – двумерное действительное линейное пространство, в котором задана система координат.

Пример III.3.Если в примере 2 вместо пар рассматривать действительные числа, то множество R есть линейное пространство над самим собой, геометрически это числовая ось.

То же самое справедливо для любого другого скалярного поля.

Пример III.4. Пусть P – множество полиномов (многочленов) переменной x с действительными коэффициентами. Под сложением полиномов будем понимать обычное их сложение по правилу приведения подобных членов, а умножение на скаляр – обычное умножение полинома на действительное число. Нейтральный элемент – полином, все коэффициенты которого равны 0. Множество полиномов с действительными коэффициентами будет действительным линейным пространством.

Пример III.5. Определим на множестве действительных чисел R сложение действительных чисел и их умножение на скаляр являющегося рациональным числом, тогда множество R будет рациональным действительным линейным пространством.