Линейная зависимость

Перейдем к описанию свойств линейных пространств.
В первую очередь к ним относятся отношения между его
элементами.

Линейной комбинацией элементов 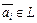над полем действительных чисел R называется элемент

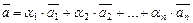, (III.1)

где , , .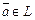

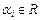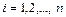Определение. Множество элементов 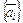, 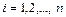называется линейно независимым, если из равенства

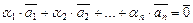, (III.2)

с необходимостью следует, что 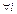, 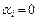. Ясно, что любая часть элементов из 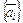также линейно независимая. Если хотя бы одно из 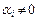, , 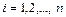то множество 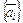называется линейно зависимым.

Пример III.6.Пусть дано векторное множество 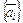. Если один из векторов 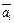, например, 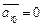, то такая система векторов линейно зависима. В самом деле, пусть множество 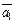, , 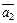…, , , 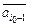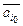…, 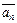линейно независимо, тогда из равенства 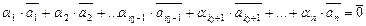следует, что .

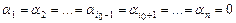Добавляя к этому множеству 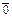вектор, умноженный на , по-прежнему имеем равенство

.

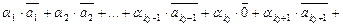
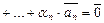Следовательно, множество векторов, как, впрочем, и любых других элементов, содержащих нулевой элемент, всегда линейно зависимо ▼.

Замечание. Если множество векторов пусто, то оно линейно независимо. В самом деле, если нет никаких индексов, то невозможно выбрать им соответствующие не равные нулю числа, чтобы сумма вида (III.2) была равна 0. Такая интерпретация линейной независимости может быть принята за доказательство, тем более что такой результат хорошо согласуется с теорией [11].

В связи со сказанным определение линейной независимости можно сформулировать так: множество элементов 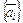линейно независимо, если 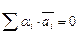и нет ни одного индекса, для которого 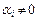. В частности, это множество может быть и пустым.

Пример III.7. Любые два скользящих вектора линейно зависимы. Напомним, что скользящими векторами называются векторы, лежащие на одной прямой. Взяв единичный вектор 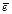, можно получить любой другой вектор умножением на соответствующее действительное число 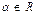, то есть 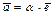или . Следовательно, уже любые два вектора в одномерном пространстве линейно зависимы.

Пример III.8. Рассмотрим пространство полиномов, где 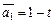, , 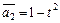, 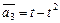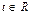. Запишем

.

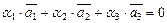Полагая 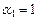, , 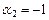, 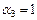получим, тождественно по t

,

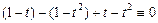то есть множество 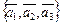линейно зависимо. Заметим, что любое конечное множество вида , 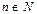линейно независимо. Для доказательства рассмотрим случай 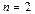, тогда из равенства

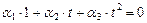, (III.3)

в случае предположения о его линейной зависимости, следовало бы, что существуют не все равные нулю числа a₁, a₂, a₃, что тождественно для любого 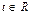выполняется (III.3), но это противоречит основной теореме алгебры: любой многочлен n-ой степени имеет не более чем n действительных корней. В нашем случае это уравнение имеет только два корня, а не бесконечное их множество. Получили противоречие.