Евклидовы пространства
Определяя линейные пространства аксиоматически, то есть абстрактно, мы для наглядности пользовались обозначениями векторных пространств, что позволило нам более отчетливо представлять свойства линейных. Эффективность этого факта проявляется и в Евклидовых пространствах.
До сих пор мы изучали качественною сторону линейных пространств, то есть строение и взаимную зависимость элементов. Перейдем к изучению их другой стороны – количественным отношениям между элементами, их измерениям. По геометрическим изображениям не более чем для 3-мерных векторных пространств мы можем количественно сравнивать векторы по длине, углу, определять расстояния между ними и т.д. Однако для пространств большей размерности такой подход неприменим, а метод аналогий ненадежен, поскольку в них уже отсутствует наглядность. Хотелось бы внутри произвольных векторных (линейных) пространств иметь такое понятие, которое было бы неизменяемым (инвариантным) при линейных преобразованиях векторов. Такое понятие, являющееся отображением векторного пространства в свое скалярное поле, называется скалярным или внутренним произведением.
Будем рассматривать линейные пространства над основным скалярным полем – полем действительных чисел R. Это наиболее важная практическая часть свойств линейных пространств. Именно здесь и проявляется более всего необходимость геометрической интерпретации их векторными.
Определение. В n-мерном линейном (вещественном) пространстве L определено скалярное умножение, если любой паре элементов 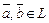 поставлено в соответствие действительное число
поставлено в соответствие действительное число 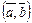 , называемое скалярным произведением элементов
, называемое скалярным произведением элементов 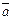 ,
, 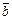 , определяемое аксиомами
, определяемое аксиомами
1) 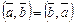 ;
;
2) 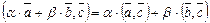 ,
, 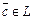 ,
, 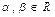 ;
;
3) 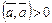 , если
, если 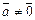 и
и 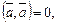 если
если 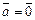 .
.
Из аксиомы 2 следует, что 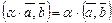 , тогда, если
, тогда, если  , то
, то 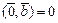 , то есть скалярное умножение нулевого элемента и любого элемента линейного пространства равно 0.
, то есть скалярное умножение нулевого элемента и любого элемента линейного пространства равно 0.
По определению положим 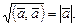
Пусть 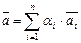 ,
, 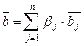 ,
,  , тогда, опираясь на аксиому 2, получим
, тогда, опираясь на аксиому 2, получим
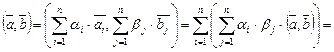
 . (III.7)
. (III.7)
Линейное пространство, в котором определено скалярное умножение, называется Евклидовым [3].
Пример III.15. Пусть в L задан базис из единичных векторов  ,
,  , …,
, …, 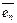 , для которых скалярное произведение
, для которых скалярное произведение 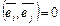 , если
, если 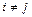 и
и 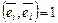 . Тогда, как следует из (III.7),
. Тогда, как следует из (III.7),
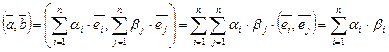 .
.
Выполнение аксиом 1) – 3) очевидно, то есть правая часть полученной формулы определяет скалярное умножение.
Следовательно, скалярное произведение можно вычислить по формуле
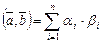 . (III.8)
. (III.8)
Упражнение. Проверить выполнение аксиом 1) – 3) для формулы (III.8).
Формула (III.7) обобщает аксиому 2) скалярного произведения на случай, когда в качестве базисных векторов выбраны произвольные векторы, однако если базисные векторы единичны и их попарное скалярное произведение равно 0 (то есть,  ,
, 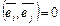 , как в формуле (III.8)), то формулу (III.8) можно принять за определение скалярного произведения, хотя здесь мы привязаны к ортогональному базису.
, как в формуле (III.8)), то формулу (III.8) можно принять за определение скалярного произведения, хотя здесь мы привязаны к ортогональному базису.
Видно, что в n-мерном пространстве скалярное умножение можно задать различными способами; все зависит от выбранного базиса. Тем не менее можно говорить, что в n-мерном векторном пространстве существует, в некотором смысле, о котором будем говорить ниже, единственное n-мерное Евклидово пространство. Подтвердим сказанное определениями, являющимися свойствами аксиом скалярного произведения.
Определение. Ненулевые векторы  ,
, 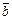 называются ортогональными, если их скалярное произведение равно 0, т.е.
называются ортогональными, если их скалярное произведение равно 0, т.е. 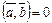 .
.
Нуль-вектор ортогонален любому вектору.
Определение. Система векторов называется ортогональной системой, если все ее векторы ортогональны между собой.
Всякая ортогональная система ненулевых векторов линейно независима [3, 11].
Ранее, основываясь на знаниях разделов школьной математики, в примерах мы рассматривали векторы, заданные координатами, и это не вызывало сомнений в справедливости такого задания. Далее будет показана непосредственная связь между различными координатными системами и скалярным произведением, здесь же отметим следующие два свойства Евклидова пространства [4, 5].
1. Всякое Евклидово пространство обладает ортогональными базисами, причем любой ненулевой вектор входит в состав некоторого ортогонального базиса.
Важным видом ортогональных базисов, соответствующих прямоугольным декартовым координатам, являются ортонормированные базисы, 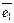 ,
, 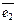 , …,
, …, 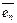 .
.
Определение. Вектор 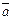 называется нормированным, если его скалярное умножение на себя равно единице, то есть
называется нормированным, если его скалярное умножение на себя равно единице, то есть
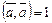 .
.
Если 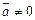 , то его нормированием называется вектор
, то его нормированием называется вектор 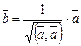 .
.
Определение. Базис 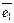 ,
, 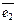 , …,
, …, 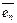 n-мерного Евклидового пространства называется ортонормированным, если он
n-мерного Евклидового пространства называется ортонормированным, если он
а) ортогонален, т.е. 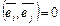 ,
,  ;
;
б) нормирован, т.е. 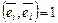 ,
, 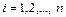 .
.
Всякое Евклидово пространство обладает ортонормированным базисом.
Определение. Евклидовы пространства  и
и 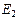 называются изоморфными, если между их векторами можно установить взаимно-однозначное соответствие, такое, что выполняются
называются изоморфными, если между их векторами можно установить взаимно-однозначное соответствие, такое, что выполняются
а)  и
и 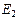 изоморфны в смысле изоморфизма их как линейных пространств: сохраняются все линейные соотношения;
изоморфны в смысле изоморфизма их как линейных пространств: сохраняются все линейные соотношения;
б) сохраняется скалярное произведение, то есть
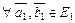 и
и 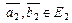 Þ
Þ 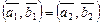 ,
,
если образами векторов 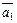 ,
, 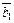 являются векторы
являются векторы 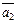 ,
, 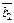 соответственно.
соответственно.
2. Отсюда следует, что любые Евклидовы пространства одинаковой размерности изоморфны. Обратное тоже справедливо.
Пример III.16. Доказать, что если скалярное произведение любых двух векторов конечного Евклидова пространства выражается формулой (III.8), то базис, относительно которого взяты координаты, является ортонормированным.
Решение.Пусть 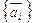 ,
, 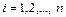 , базис n-мерного Евклидова пространства
, базис n-мерного Евклидова пространства  и
и 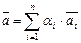 ,
, 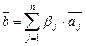 . Сначала покажем, что он ортогонален. Имеем по формуле (III.7)
. Сначала покажем, что он ортогонален. Имеем по формуле (III.7)
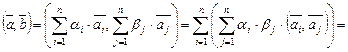
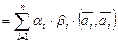 .
.
Отсюда следует, что, если 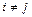 , то
, то  , поэтому базис ортогонален.
, поэтому базис ортогонален.
Покажем, что он нормирован. Учитывая условие (формула (III.8)), получаем

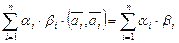 .
.
Отсюда 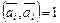 ,
, 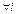 , то есть базис нормированный.
, то есть базис нормированный.
Выполнение обоих условий ортонормированности базиса доказано ▼.
Дата добавления: 2016-01-26; просмотров: 1418;
