IV. Векторная алгебра

Векторы

Величина, которая полностью определяется своим числовым значением, называется скалярной или скаляром (термин ввел У. Гамильтон в 1843 г.). Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора, который ранее уже использовался в примерах.

Вектор – это направленный отрезок. Если А – начало вектора, а В – его конец, то вектор обозначается символом 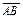или . Вектор, 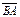называется противоположным вектору 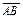. Вектор противоположный вектору ,обозначается ( ).

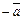Длиной вектора 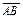называется длина отрезка 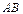и обозначается 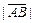. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 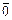(или 0, когда нет сомнений в понимании обозначения). Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным и обозначается через 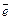. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора . Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Два вектора и называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку O пространства, то есть векторы определены с точностью до параллельного переноса.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.