Глава 14. ИНФОРМАЦИОННЫЙ ПОИСК И ИССЛЕДОВАНИЕ ПРОСТРАНСТВА СОСТОЯНИЙ

В отличие от неинформационной стратегии поиска решения задач путем систематической выборки новых состояний и их проверки применительно к цели, мало эффективной в большинстве случаев, при информационной стратегии поиска используются знания, относящиеся к конкретной задаче [3]. В общем алгоритме, структура которого представляется в виде дерева или графа, во многих случаях для развертывания целесообразно выбирать узел с наименьшей функцией оценки f(n), поскольку такая оценка измеряет расстояние до цели. При этом поиск осуществляется в рамках общей инфраструктуры с помощью очереди по приоритету, поддерживающей периферию в возрастающем порядке f-значений.
Процедура исследования пространства состояний заключается в поиске наилучшего узла в соответствии с принятой функцией оценки, неудачный выбор которой может завести поиск в тупик.

В семействе алгоритмов «поиска по первому наилучшему совпадению» используются различные эвристические функции h(n) – оценки стоимости наименее дорогостоящего пути от узла n до целевого. Дальнейшее рассмотрение этой задачи ограничивается только двумя наиболее распространенными способами использования эвристической информации для управления поиском.

14.1. ЖАДНЫЙ «ПОИСК ПО ПЕРВОМУ НАИЛУЧШЕМУ
СОВПАДЕНИЮ»

Вариантжадного «поиска по первому наилучшему совпадению» использует простейшую эвристическую функцию оценки узлов f(n) = h. Так задача поиска маршрута в Румынии решается на основе эвристической функции определения расстояния по прямой линии h_SLD в узловых точках маршрута до Бухареста с одним ограничением: если n – целевой узел, то h(n) = 0. Предполагается наличие априорных сведений о расстояниях по прямой линии от каждого прочего города до Бухареста (рис. 32).

При определении пути от Арада до Бухареста с использованием эвристической функции h_SLD первым узлом, подлежащим развертыванию из узла Арад, является узел Сибиу, поскольку город Сибиу находится ближе к Бухаресту, чем города Зеринд или Тимишоара. Далее развертыванию подлежит узел Фэгэраш, так как теперь именно он ближайший к Бухаресту и обеспечивает формирование целевого узла Бухарест. Данный алгоритм позволяет найти решение рассмотренной задачи, однако само найденное решение не оптимально: путь до Бухареста через города Сибиу и Фэгэраш на 32 километра длиннее, чем через города Рымнику-Вылча и Питешти.

Восприимчивость процедуры минимизации h(n) к фальстартам, при которых приходится отменять начальные этапы, проиллюстрируем на примере решения задачи поиска пути от города Яссы (I) до города Фэгэраш (F) (рис. 33).При использовании эвристической функции h(n) в первую очередь должен быть развернут узел города Нямц (N), поскольку он является ближайшим к узлу Fagaras, но этот путь становится тупиковым. Единственное решение состоит в том, чтобы отправиться вначале в город Васлай (V), что согласно данной эвристической функции уводит дальше от цели, а затем продолжать движение через Урзичени (U) и Бухарест (B) в Фэгэраш. Помимо развертывания ненужных узловпри использовании эвристической функции h(n) процедура поиска станет совершать возвратно-поступательные движения между узлами Нямц и Яссы и решение никогда не будет найдено, если не предусмотреть обнаружение повторяющихся состояний.

Как и поиск «в глубину», алгоритм «жадный поиск по первому наилучшему совпадению» не является оптимальным, поскольку к цели постоянно следуют по единственному пути, а возвращаются к предыдущим узлам только в случаях попадания в тупик. К тому же он является не полным, поскольку способен отправиться по бесконечному пути, да так и не вернуться, чтобы опробовать другие возможности. Эту сложность можно преодолеть надлежащим выбором эвристической функции.

14.2. МИНИМИЗАЦИЯ СУММАРНОЙ ОЦЕНКИ
СТОИМОСТИ РЕШЕНИЯ (поискA^*)

В более рациональной разновидности «поиска по первому наилучшему совпадению» (поиск 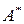) применяется оценка узлов, объединяющая в себя стоимость достижения данного узла g(n)истоимость прохождения от данного узла до цели h(n):

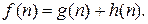
Поскольку функция g(n)определяет стоимость пути от начального узла до n-го узла, а функция h(n)оценивает стоимость наименее затратного пути от узла 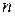до цели, то справедливо следующее утверждение: f(n) – это оценка стоимости наименее дорогостоящего пути решения, проходящего через узел n. Поиск A^*считается полным и оптимальным, если определено наименее дорогостоящее решение. Для этого необходимо вначале проверить узел, для которого функция f(n) имеет наименьшее значение, а эвристическая функция h(n) удовлетворяет некоторым условиям.

Допустимая эвристическая функция h_SLD определяется расстоянием по прямой линии, соединяющей выбранный узел и целевой, что соответствует минимально возможному расстоянию. Пусть g(n) – точная стоимость достижения узла n, а функция h(n) (следовательно, и f(n)) никогда не переоценивает истинную стоимость достижения решения через узел 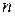, тогда поиск A^*в сочетании с алгоритмом «поиск по дереву» является оптимальным. На рис. 32 показан процесс поиска A^*пути в Бухарест с помощью дерева. Значения gвычисляются на основании стоимостей
этапов, показанных на рис. 32, а значения функции h_SLD приведены в
табл. 14

Следует отметить, что узел Bucharest впервые появляется в периферии на этапе, показанном на рис. 32, д., но не выбирается для развертывания, поскольку его f – стоимость (450) выше, чем стоимость узла Pitesti (417). Алгоритм не останавливается на решении со стоимостью 450, поскольку может существовать решение, при котором путь через город Питешти имеет стоимость 417. Приведенный пример свидетельствует, что поиск A^*с использованием алгоритма «поиск по дереву» является оптимальным, если функция h(n) допустима.

Таблица 14