III. Линейные пространства
Ранее отмечалось, что многие множества, существенно различаясь по природе своих элементов, имеют одинаковые свойства, то есть могут быть описаны, с точки зрения современной алгебры, единой системой аксиом. Наиболее востребован практикой оказался класс множеств, обладающих свойствами линейного пространства. Часто их называют векторными, поскольку векторные величины получили широкое распространение в различных научно-практических исследованиях и приложениях. Кроме того, векторные пространства геометрически наглядны, что делает линейные пространства понятными, расширяя тем самым область использования их в науке и практических исследованиях.
Во введении понятие числового поля определялось аксиоматически. Рассмотрены поля рациональных чисел Q, действительных чисел R и комплексных чисел C. В этом разделе введем аксиоматически линейные пространства.
Пусть дано любое числовое поле и все скаляры являются его элементами [11].
Определение. Линейным пространством над числовым полем, например R, называется множество L элементов, удовлетворяющее аксиомам:
A)Для любой пары 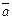 ,
, 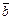 элементов из L всегда найдется элемент
элементов из L всегда найдется элемент 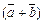 , называемый суммой элементов
, называемый суммой элементов 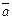 и
и 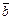 , что выполняется
, что выполняется
1) 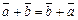 (коммутативность);
(коммутативность);
2) 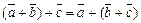 (ассоциативность);
(ассоциативность);
3)существует нейтральный элемент 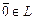 , называемый начальным, такой, что
, называемый начальным, такой, что 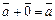 ;
;
4)каждому элементу 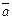 соответствует однозначно определенный элемент
соответствует однозначно определенный элемент 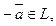 такой, что
такой, что 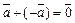 .
.
B)Для любой пары из a, b и 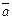 ,
, 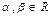 ,
, 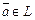 найдется элемент
найдется элемент 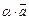 ,
, 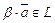 , называемый произведением a и
, называемый произведением a и 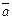 или b и
или b и 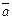 соответственно, такой, что
соответственно, такой, что
5) 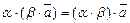 (ассоциативность умножения на скаляры);
(ассоциативность умножения на скаляры);
6) 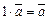 .
.
7) 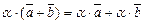 – умножение на скаляры дис-трибутивно (сочетательно) относительно сложения;
– умножение на скаляры дис-трибутивно (сочетательно) относительно сложения;
8) 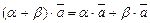 – умножение на элементы дис-трибутивно относительно сложения скаляров.
– умножение на элементы дис-трибутивно относительно сложения скаляров.
Отношения между линейным пространством L и полем скаляров выражают словами: линейное пространство L над полем скаляров.
В дальнейшем под полем скаляров будем понимать основное поле R действительных чисел, а имея дело с линейными пространствами в обозначениях и геометрической интерпретации, будем использовать векторные обозначения, что и было сделано в аксиомах.
Вектор (лат. vector – скользящий) – в геометрическом пространстве определяется как отрезок прямой, имеющий направление; задается упорядоченно: начало вектора (точка A) и конец (точка B). Для обозначения такого вектора используются а) пара букв 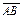 или
или 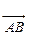 , а также одна буква
, а также одна буква 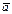 или a (полужирный шрифт), б) на рисунках как направленный отрезок прямой. Таким образом, векторные обозначения и геометрические векторы – суть обозначения элементов линейного пространства.
или a (полужирный шрифт), б) на рисунках как направленный отрезок прямой. Таким образом, векторные обозначения и геометрические векторы – суть обозначения элементов линейного пространства.
Рассматривают геометрические векторные пространства трех видов векторов: связанные, скользящие и свободные. В пространстве свободных векторов достаточно иметь одинаковые направления; скользящие векторы лежат на одной прямой; связанные векторы имеют общее начало. Длина для всех видов векторов определяется его модулем - 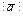 . Из условия упорядоченности обозначений вектор
. Из условия упорядоченности обозначений вектор 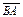 противоположен вектору
противоположен вектору 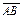 . Вектор, у которого начало совпадает с концом, например
. Вектор, у которого начало совпадает с концом, например 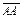 , называется нуль-вектором,
, называется нуль-вектором, 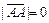 , то есть обозначение совпадает с числом 0; ему приписывают любое направление. Вектор
, то есть обозначение совпадает с числом 0; ему приписывают любое направление. Вектор 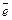 , длина которого
, длина которого 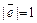 , называется единичным, помимо этого свойства, он выполняет функции масштаба.
, называется единичным, помимо этого свойства, он выполняет функции масштаба.
Векторы называются коллинеарными, если они лежат в одной или в параллельных прямых, и компланарными, если лежат в одной или параллельных плоскостях.
Зададим вектор (свободный) аксиоматически. Определим векторное пространство как понятие, обобщающее понятие совокупности всех векторов обычного трехмерного пространства. Элементы числового поля будем называть по-прежнему скалярами.
Определение.Векторным пространством над скалярным полем P называется множество L векторов, в котором определена операция сложения векторов и операция умножения векторов на скаляры из основного поля P, задаваемых аксиомами:
A.Сложение. 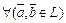 ,
, 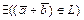 , называемый суммой векторов
, называемый суммой векторов 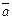 и
и 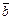 , что
, что
1) 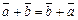 ;
;
2) 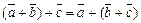 ;
;
3)существует нулевой вектор 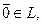 такой, что
такой, что 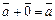 ;
;
4)для вектора 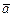 найдется единственный противоположный вектор
найдется единственный противоположный вектор 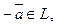 такой, что
такой, что 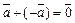 ;
;
B.Умножение. 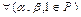 ,
, 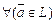 Þ $ вектор
Þ $ вектор 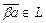 , называемый произведением скаляра b и вектора
, называемый произведением скаляра b и вектора 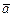 , что
, что
5) 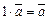 ;
;
6) 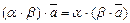 ;
;
C.Умножение дистрибутивно относительно
7)сложения векторов, 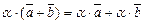 ;
;
8)сложения скаляров, 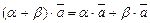 .
.
Из аксиом вытекают важные свойства векторов L ( 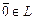 ):
):
1) 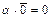 ; то есть умножение нуль–вектора на скаляр дает число 0;
; то есть умножение нуль–вектора на скаляр дает число 0;
2) 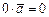 ; умножение числа 0 на вектор дает также число 0;
; умножение числа 0 на вектор дает также число 0;
3) 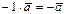 , то есть чтобы получить вектор, противоположный заданному, достаточно умножить его на -1.
, то есть чтобы получить вектор, противоположный заданному, достаточно умножить его на -1.
Аксиомы 1) – 4) образуют абелеву группу, а аксиомы
5) – 8) отражают тот факт, что умножение элементов на скаляры является линейной функцией (оператором, преобразованием) элементов из L. Это подтверждает не только внешнее сходство аксиом поля и векторного пространства, но и их внутреннюю связь, другими словами, понятия линейное пространство и векторное пространство – изоморфны.
Пример III.1.Рассмотрим множество векторов на плоскости. Покажем, что оно образует линейное пространство L2 над полем чисел R. Достаточно проверить выполнение аксиом 1) – 8). Проверку осуществим, используя геометрические образы. Исходя из определения свободных векторов 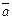 ,
, 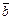 , совместим параллельным переносом конец вектора
, совместим параллельным переносом конец вектора 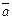 с началом вектора
с началом вектора 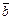 , а затем – начало вектора
, а затем – начало вектора 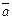 с концом вектора
с концом вектора 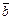 . Полученный вектор
. Полученный вектор 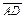 назовем суммой векторов
назовем суммой векторов 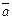 и
и 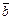 (рис. III.1), то есть
(рис. III.1), то есть 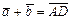 .
.
Положим 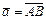 , тогда
, тогда 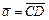 , аналогично
, аналогично 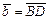 , тогда
, тогда 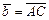 (рис. III.1).
(рис. III.1).
А. Сложение. Если векторы неколлинеарные, то по «правилу треугольников» сложения векторов, имеем
1) 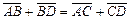 .
.
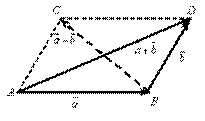
Рис. III.1
Для коллинеарных векторов это очевидно, так как DADB вырождается в отрезок прямой.
2) 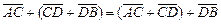 или
или 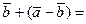
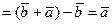 .
.
Тот факт, что векторы параллелограмма попарно равны, не является принципиальным. Для общего случая, можно рассмотреть любой четырехугольник на плоскости.
3) Очевидно, если обозначить 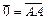 ;
;
4) Следует из доказательства аксиомы 2.
B. Умножение.Пусть 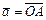 лежит на прямой (рис. III.2).
лежит на прямой (рис. III.2).
5) 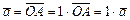 ;
;

Рис. III.2
6) положим 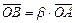 , а
, а 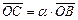
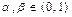 (рис.2), тогда
(рис.2), тогда 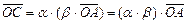 или
или 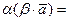
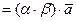 .
.
Дата добавления: 2016-01-26; просмотров: 1642;
