VI. Линейные операторы
Линейный оператор
В линейной алгебре, помимо векторных пространств, фундаментальное значение имеют линейные операторы (или линейные преобразования) [1, 7, 11].
Как общее понятие, оператор – отображение одного множества на другое, каждое из которых наделено некоторой структурой (системой аксиом, отношением порядка, алгебраической операцией и т.д.). Аналогом оператора в математическом анализе является функция.
Современное определение линейного оператора A принадлежит Дж. Пеано для векторных пространств с основным полем R действительных чисел, с областью определения и областью значений в L.
Отметим, что при использовании современной вычислительной техники (кластеров, вычислительных систем, нейронных систем) эффективность параллельных программ существенно повышается, если представленные для решения задачи записаны в векторной (операторной) форме.
Поскольку линейный оператор рассматривается как отображение 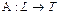 ,
, 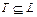 или как функция
или как функция 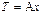 , то в дальнейшем, векторы будем обозначать малыми буквами x, y, …, возможно с индексами,
, то в дальнейшем, векторы будем обозначать малыми буквами x, y, …, возможно с индексами, 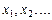 .
.
Определение. Линейным оператором A на векторном пространстве L называется линейное преобразование одного вектора в другой из того же пространства, так что выполняются свойства линейности
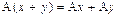 ,
,
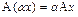 , (VI.1)
, (VI.1)
что эквивалентно линейной комбинации,
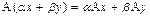 ,
, 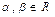 . (VI.2)
. (VI.2)
Из (VI.1) следует, что среди линейных операторов существуют:
а) нулевой, 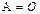 , то есть такой, что
, то есть такой, что 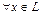 ,
, 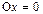 , где
, где
0 – нулевой вектор;
б) единичный (тождественный) 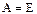 , то есть такой, что
, то есть такой, что 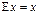 ;
;
в) подобия P, то есть такой, что 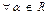
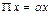 ,
,
отсюда следует, что при 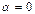 получаем нулевой оператор, а при
получаем нулевой оператор, а при 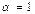 тождественный.
тождественный.
Из (VI.2) следует, что 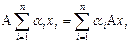 , где
, где 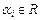 ,
, 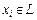 . Область значений
. Область значений 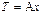 оператора A является подпространством, в частности множество векторов
оператора A является подпространством, в частности множество векторов 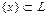 , таких что
, таких что 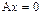 – подпространство.
– подпространство.
Множество 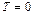 называется ядром оператора A, а размерность ядра называется дефектом оператора A.
называется ядром оператора A, а размерность ядра называется дефектом оператора A.
Пример VI.1. Пусть в векторном пространстве L задан базис. Оператор A ставит в соответствие каждому вектору x его координату с фиксированным номером. Доказать, что A – линейный оператор.
Доказательство. Пусть 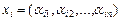 ,
, 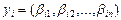 , тогда, например,
, тогда, например, 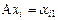 ,
, 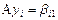 , покажем, что
, покажем, что
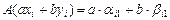 ,
, 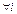 .
.
В самом деле, имеем из (VI.2),
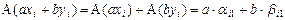 . ▼
. ▼
Дата добавления: 2016-01-26; просмотров: 1429;
