Угол между плоскостями

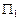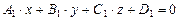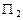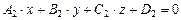Пусть даны две плоскости : и : . Найдем угол между этими плоскостями, который совпадает с углом между их нормальными векторам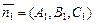и и .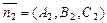

Учитывая, что

,

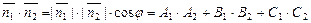получим

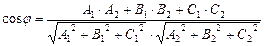. (V.17)

Пример V.17. Даны координаты вершин пирамиды 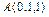, , 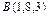, 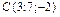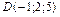. Найти: 1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС; 3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.

Решение.

1).Длина ребра AB совпадает с длиной вектора 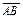, поэтому определим координаты векторов 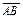и .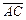

, .

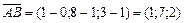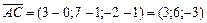Длина вектора равна корню квадратному из суммы квадратов его координат, то есть

, .

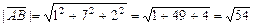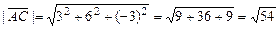2).Угол между ребрами AB и AC совпадает с углом между векторам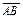и и 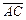, который можно определить по формуле

, .

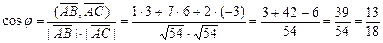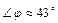3).Грань ABC представляет собой треугольник, его площадь найдем через векторное произведение:

,

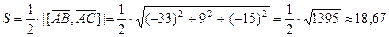так как

.

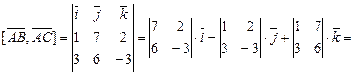
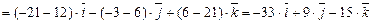4).Объем пирамиды вычислим по формуле:

.

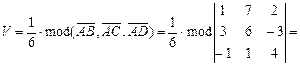
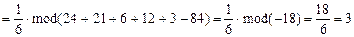Здесь .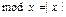

5).Уравнение прямой, проходящей через точки А, В, имеет вид:

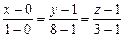, то есть, .

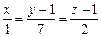6).Уравнение плоскости ABC определим из равенства

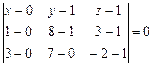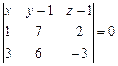, или

.

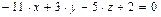7).Так как высота – это прямая перпендикулярная плоскости ABC, ее направляющим вектором будет вектор-нормаль 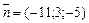плоскости ABC, тогда уравнение высоты имеет вид:

.

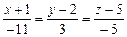Выполним чертеж (рис. V.11).

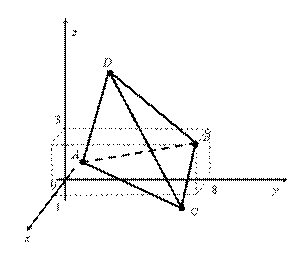
Рис. V.11