Взаимное расположение плоскостей
Пусть две плоскости заданы в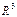 
общими уравнениями
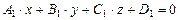и 
,
, 
.
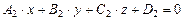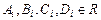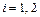Эти плоскости параллельны только в том случае, если коллинеарны их нормальные векторы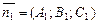 
и 
, то есть выполняются условия: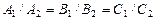 
.
Следовательно, две плоскости, заданные общими уравнениями, параллельны, если коэффициенты при одноименных переменных пропорциональны.
Если кроме коэффициентов при переменных пропорциональны и свободные члены, то есть выполняются равенства
,
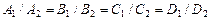то плоскости совпадают.
Чтобы две плоскости пересекались, необходимо и достаточно, чтобы коэффициенты при переменных x, y, z не были пропорциональны.
Плоскости перпендикулярны в том случае, если перпендикулярны их нормальные векторы, то есть выполняется условие:
.
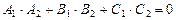Пример V.8.Установить, перпендикулярны ли плоскости,
заданные уравнениями 
и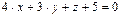 
.
Решение. Плоскости перпендикулярны в том случае, если их нормальные векторы 
и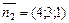 
удовлетворяют условию 
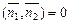. Так как 
, то указанное условие выполнено и значит, данные плоскости перпендикулярны.
Уравнение прямой в пространстве R3
Каноническое уравнение прямой. Положение прямой вполне определено, если заданы лежащая на ней точка и направление. Направление прямой может быть задано любым вектором коллинеарным данной прямой, который называется направляющим вектором.
Выведем уравнение прямой a, проходящей через данную точку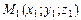 
и имеющей направляющий вектор 
.
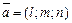Произвольная точка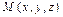 
лежит на прямой a только в том случае, если векторы 
и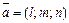 
коллинеарны, то есть для них выполняется условие:
.
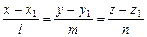Эти равенства (а этими равенствами фактически заданы два независимых уравнения) определяют прямую (рис. V.7), проходящую через заданную точку 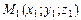коллинеарно вектору 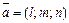, и называются каноническим уравнением прямой в пространстве.
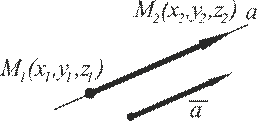
Рис. V.7
Числа l, m и n являются проекциями направляющего вектора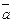 
на координатные оси. Так как вектор 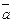– ненулевой, то все три l, m и n числа не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю, например,
,
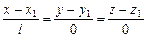которая означает, что проекции вектора 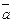на оси Oy и Oz равны нулю. Поэтому и вектор 
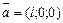, и прямая, заданная указанным образом, перпендикулярны осям Oy и Oz, то есть плоскости Оyz.
Пример V.9.Составить уравнение прямой, перпендикулярной плоскости 
и проходящей через точку пересечения этой плоскости с осью Oz.
Решение.Найдем точку пересечения данной плоскости с осью Oz. Так как любая точка, лежащая на оси Oz, имеет координаты (0; 0; z), то, полагая в заданном уравнении плоскости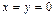 
, получим 
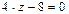или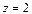 
. Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты
(0; 0; 2). Поскольку искомая прямая перпендикулярна плоскости, то, тем самым, она параллельна ее нормальному вектору 
. Поэтому направляющим вектором прямой может служить вектор нормали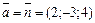 
заданной плоскости.
Теперь запишем искомые уравнения прямой, проходящей через точку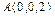 
в направлении вектора 
:
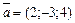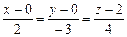или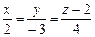 
.
Дата добавления: 2016-01-26; просмотров: 2404;