Взаимное положение двух прямых на комплексном чертеже

Если через данную точку А требуется провести прямую, параллельную данной прямой LМ,то построение сводится к проведннию через точку А прямой, параллельной L"M", и через точку А' прямой параллельной L'M', рис.2.9 а.

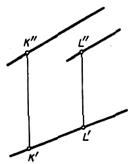
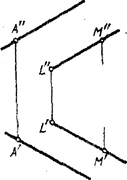
В случае, изображенном на рис.2.9 б, параллельные прямые расположены в общей для них проецирующей плоскости, перпендикулярной к пл.Н, Поэтому горизонтальные проекции этихпрямых расположены на одной прямой.

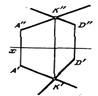
Еслипрямые пересекаются в точке К, то их проекции тоже пересекаются, при этом проекции точки К' и К" расположены на одном перпендикуляре (рис.2.10).

Действительно, если точка К принадлежит обеим прямым АВ и CD, то проекция этой точки должна быть точкой пересечения проекций данных прямых,

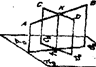
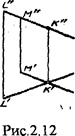
Заключение о том, что данные на чертеже прямые пересекаются между собой, можно сделать всегда по отношению к пря-мым общего положения, независимо от того, даны ли проекциина трех или двух плоскостях проекций, необходимым и достаточным условием является лишь то, чтобы точки пересечения одноименных проекций находились на одном и том же перпендикуляре к соответствующей оси проекций (рис.2.11) или. на чертеже без оси проекций (рис.2,12), эти точки оказались бы налинии связи установленного для нее направления. Но если однаиз данных прямых параллельна какой- либо из плоскостей проекций, а на чертеже не даны проекции на этой плоскости, тонельзя утверждать, что такие прямые пересекаются между со-бой, хотя бы и было соблюдено указанное выше условие, на-пример, в случае, данном на рис.2.13, прямые АВ и CD, из ко-торых прямая CD параллельна плоскости W, не пересекаются между собой; это может быть подтверждено построением профильных проекций или применением правила о делении отрез-ков в данном отношении.

а) б)

Рис.2.9

Если точка пересечения npoeкцuu прямых не расположены на одном перпендикуляре к оси х, то прямыескрещиваются (рис.2.14).

На рис.2.14, 2.15 изображены две скрещивающиеся прямые общего положения: хотя одноименные проекции и пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, то есть прямые не пересекаются между собой.

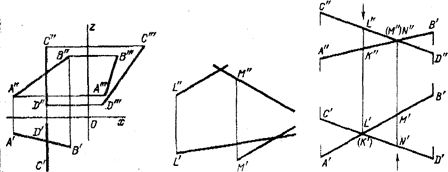
Рис.2.13. Рис.2.14 Рис. 2.15