Параллельное проецирование

ВИДЫ ПРОЕЦИРОВАНИЯ

Существует несколько видов проецирования.

Проекциицентральные, - когда задается плоскость про-екции и центр проекции точки, не лежащей в этой плоскости(рис. 1.1).

Рис. 1.1 Рис. 1.2

Параллельное проецирование

Параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекции (рис. 1.2).

Параллельные проекции также называют цилиндрическими, которые в свою очередь делятся на: косоугольные и прямоугольные.

В параллельных проекциях, также как и в центральных:

1) для прямой линии проецирующей поверхностью в общем случаеслужит плоскость, и поэтому прямая линия вообще проецируется в виде прямой;

2) каждая точка и линия в пространстве имеют единственную своюпроекцию;

3) каждая точка на плоскости проекций может быть проекцией множества точек, если через них проходит общая для них проецирующая прямая;

4) каждая линия на плоскости проекций может быть проекцией множества линий, если они расположены в общей для них проеци-рующей плоскости;

6

5) для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию,

6) если точка Î прямой, то проекция точки принадлежит проекции этой прямой; (рис. 1.3) точка К принадлежит прямой (проекция К⁰ принадлежит проекции этой прямой),

7) если прямая (АВ) параллельна направлению проецирования, то проекцией прямой является точка А°, она же В° (рис. 1.3),

8) отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину (CD = C°D° , как отрезки параллельных прямых между параллельными прямыми), (рис. 1.3).

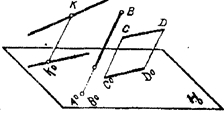
Рис. 1.3

В данном курсе преимущественно рассматриваются прямоугольные проекции (слово прямоугольные часто заменяют на ортогональные, образованное от греческих слов прямой и угол).

Точка.

Точка относится к основным неопределяемым понятиям геометрии. Точка не имеет размеров; это основной геометрический элемент линии и поверхности.

Положение точки (и любой геометрической фигуры) в пространстве может быть определено, если будет задана координатная система отнесения. Наиболее удобная является декартовая система координат (французский философ, математик Декарт 1596 - 1650 г.) состоящая из трех взаимно перпендикулярных плоскостей, при этом получается восемь октантов (рис. 1.4).

7

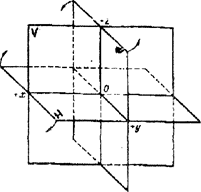
Рис. 1.4

Рис. 1.5

Преобразование в эпюр осуществляется совмещением плоскостей путем вращения (рис. 1.5), Или условно можно принять для построения одну из четвертей.

Рассмотрим принятую систему расположения плоскостей проекций (рис. 1.6).

Условимся называть: плоскость - Н- горизонтальная плоскость проекции, V- фронтальная плоскость проекции, W-профильная плоскость проекции.

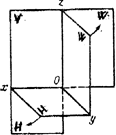
Рис. 1.6