Параллельное проектирование и его свойства.

Пусть в пространстве дана некоторая плоскость a и вектор 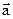, который ей не параллелен.

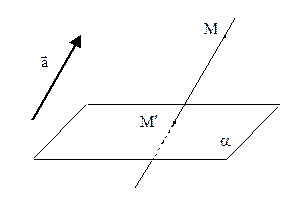Определение 1. Под параллельной проекцией точки М на плоскость a в направлении вектора 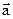понимается точка М¢, полученная при пересечении плоскости a и прямой, параллельной 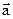и проходящей через М.

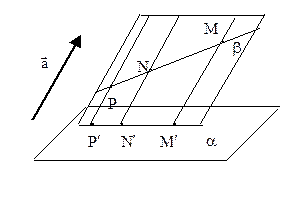Если в пространстве дана некоторая фигура, то, проектируя каждую ее точку, мы получим параллельную проекцию этой фигуры на плоскость.

Параллельное проектирование обладает следующими свойствами.

1. 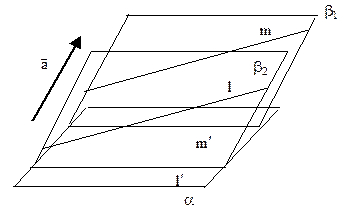Коллинеарные точки отображаются в коллинеарные и сохраняется их простое отношение.

2. Прямая проектируется в прямую, отрезок – в отрезок, луч – в луч.

3. Параллельные прямые отображаются либо в параллельные прямые, либо в одну прямую.

4. Сохраняется отношение длин отрезков, лежащих на одной прямой или на параллельных прямых.

Изображение плоских и пространственных фигур при параллельном проектировании

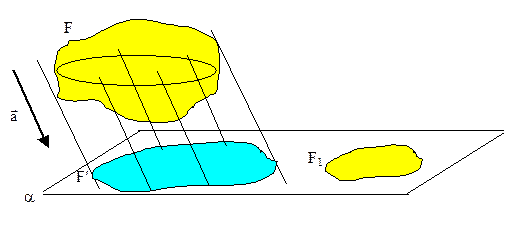Определение. Фигура F₁ плоскости изображения, подобная F¢, называется изображением фигуры F при параллельном проектировании.

Введем понятие аффинного отображения одной плоскости на другую.

Взаимно однозначное отображение плоскости a на плоскость b называется аффинным, если при этом отображении коллинеарные точки отображаются в коллинеарные и сохраняется простое отношение точек.

Основное свойство аффинных отображений. Пусть на плоскости a дан аффинный репер R, а на плоскости b - аффинный репер R¢. Тогда существует единственное аффинное отображение плоскости a на плоскость b, при котором репер R отображается в репер R¢.

Будем считать, что фигура F плоскости a аффинно эквивалентна фигуре F¢ плоскости b, если существует аффинное отображение a на b, при котором образом F служит фигура F¢.

Из основного свойства аффинных отображений следует, что два треугольника, один из которых принадлежит плоскости a, а другой плоскости b, аффинно эквивалентны.

Два четырехугольника АВСD и A¢B¢C¢D¢, один из которых принадлежит плоскости a, а другой плоскости b, аффинно эквивалентны в том и только в том случае, когда (АС,О) = (A¢C¢,O¢), (BD,O) = (B¢D¢,O¢), где О и O' - соответственно точки пересечения их диагоналей AC и BD, А¢С¢ и В¢D¢.

Доказательства этого утверждения проводится дословно так же, как и в случае аффинных преобразований плоскости.

Справедлива следующая теорема.

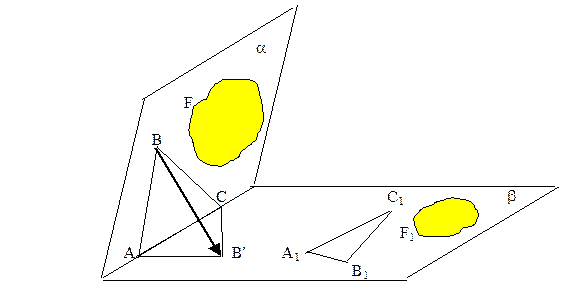Теорема. Фигура F₁ плоскости b служит изображением фигуры F плоскости a в ом и только в том случае, когда они аффинно эквивалентны.

Треугольник изображается треугольником.

Четырехугольник – четырехугольником, точка пересечения диагоналей которого делит диагонали в том же отношении, что и у оригинала.

Поэтому прямоугольник, квадрат, ромб и параллелограмм изображаются параллелограммом.

Трапеция изображается трапецией, отношение оснований которой совпадает с отношением оснований оригинала.

Произвольный n – угольник изображается n – угольником. Рассмотрим пятиугольник ABCDE плоскости a, который изображается пятиугольником A₁B₁C₁D₁E₁ плоскости b. Треугольник ABC изображается произвольным треугольником A₁B₁C₁, а точки D₁E₁

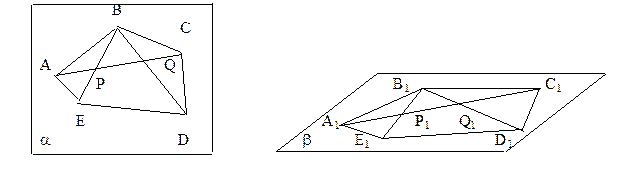строятся следующими образом: точки пересечения диагонали A₁C₁ с диагоналями B₁E₁ и B₁D₁делит их в том же отношении, что и у оригинала.

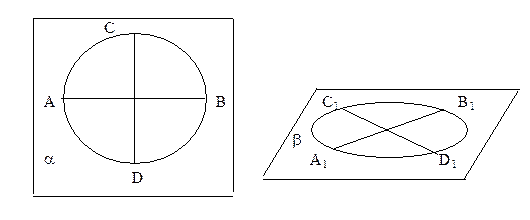Так как эллипс и окружности аффинно эквивалентны, то окружность изображается эллипсом, а ее перпендикулярные диаметры – сопряженными диаметрами эллипс, а центр - центром.

Теорема Польке – Шварца. Вершины любого четырехугольника A₁B₁C₁D₁ плоскости b, заданные в определенном порядке служат изображением аффинного репера, равного данному R(A,B,C,D).

12 3

Дата добавления: 2016-02-02; просмотров: 2166;