Изображение пространственных фигур.
Изображение цилиндра.
 |
Дан прямой круговой цилиндр. Основания цилиндра изобразятся эллипсами, а его образующие АА¢ и ВВ¢ - касательными к изображению оснований (контурные образующие).
 |
При проекции конуса на плоскость a мы получим, что окружность основания изображается эллипсом, изображение вершины S принадлежит прямой, содержащей ее меньшую ось, а контурные образующие – отрезками касательных, проведенных из изображения вершины к изображению окружности основания.
Изображение сферы. При построении изображения сферы используется ортогональная проекция. Поэтому изображением сферы служит окружность. Для наглядности на изображении сферы указывают окружность большого круга, не перпендикулярную и не параллельную плоскости изображения (экватор). Проведем прямую, перпендикулярную плоскости экватора. Изображения ее точек пересечения со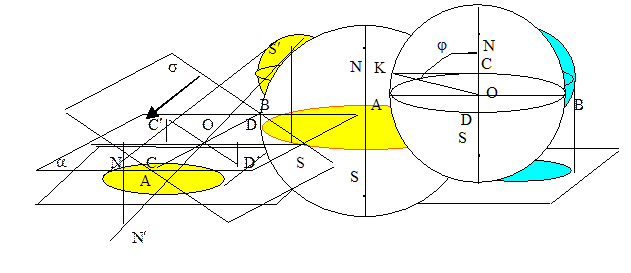 
сферой называются полюсами. Полюсы сферы не расположены на контурной окружности сферы, иначе экватор сферы представляет собой отрезок, а его плоскость – параллельна плоскости изображения. Укажем способ построения полюсов, соответствующих данному экватору.
Обозначим плоскость изображения через a, а плоскость экватора через s. АВ и CD оси эллипса экватора на изображении. Они принадлежат плоскости a, Точки С¢ и D¢ принадлежат большой окружности, полученной при пересечении s и сферы. Эти точки проектируются в С и D. Прямая S¢N¢ перпендикулярна плоскости s, а сами эти точки служат пересечением прямой и сферы. Таким образом: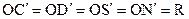 
Величина угла между плоскостями a и s равна j. Очевидно, этот угол совпадает по величине с углом СОС¢ прямоугольного треугольника СОС¢, а угол NON¢ прямоугольного треугольника NON¢ равен 
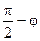. Отсюда следует, что 
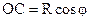, а 
.
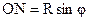С другой стороны, если СК – касательная к эллипсу экватора на изображении сферы, то треугольник СОК прямоугольный,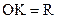 
, и, как было доказано ранее, 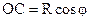. Поэтому 
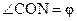. Отсюда следует, что 
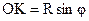. Таким образом,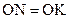 
Дата добавления: 2016-02-02; просмотров: 1503;