Виды опор и неизменяемость пространственных ферм

Понятие о пространственных системах

Пространственными называют такие шарнирно-стержневые системы, элементы которых расположены не в одной плоскости. Все сооружения являются пространственными, но многие из них можно расчленить на отдельные плоские системы, работающие независимо. Существуют все же такие пространственные системы, которые невозможно разложить на отдельные плоские системы (различные башенные и крановые конструкции, купола и др.).

Пространственные системы по характеру образования делятся на следующие основные виды: рамы, оболочка и фермы.

Рама (рис. 1.8..1) представляет собой пространственное жесткое сочленение стержней между собой в узлах.

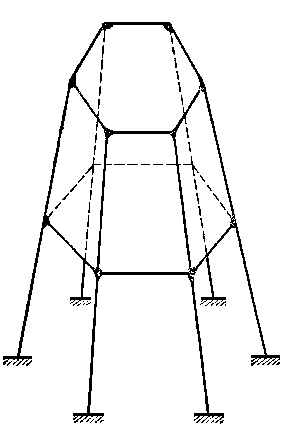
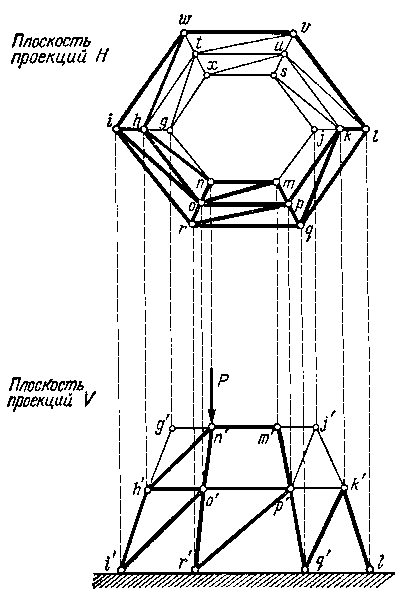
Рисунок 1.8..1. Рисунок 1.8..2.

Оболочка — пространственная тонкостенная конструкция, срединная поверхность которой криволинейна.

Пространственная ферма — геометрически неизменяемая система стержней, соединенных между собой пространственными шарнирами. На рис. 1.8.2 в двух проекциях показана пространственная шарнирно-стержневая статически определимая ферма в виде купола. От действия вертикальной силы Р, приложенной в узле n, возникают усилия в стержнях nm, no, nh, mo, mp, hw, hi, ho и т.д.

При расчете пространственных ферм предполагается, что все стержни фермы соединены в узлах идеальными шаровыми шарнирами, обеспечивающими вращение концов вокруг трех взаимно перпендикулярных осей. Нагрузку, действующую на ферму, принимают узловой. Следовательно, в стержнях пространственной фермы возникают лишь продольные усилия.

Виды опор и неизменяемость пространственных ферм

Типы опор пространственных ферм:

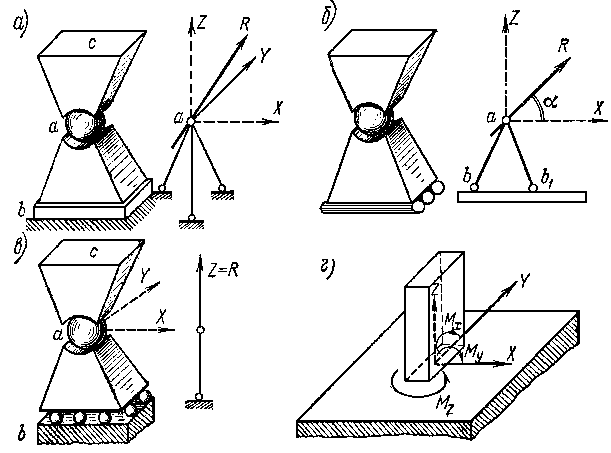
Рисунок 1.8.3

Опора первого типа — шарнирно неподвижная шаровая опора (рис. 1.8.3, а). Шаровой вкладыш этой опоры а находится в сферических углублениях верхнего и нижнего балансиров, неподвижно прикрепленных соответственно к узлу с пространственной системы и опорной подушке b. Реакция такой опоры проходит через центр шарнира и имеет три составляющие Х, Y, Z (см. условное изображение этого типа опоры в виде трех стержней, не лежащих в одной плоскости, на рис. 1.8.3, а справа). Зная составляющие Х, Y, Z полной реакции опоры R, находим ее значение.

Опора второго типа—подвижная цилиндрическая опора (рис. 1.8.3, 6)—отличается от предыдущей тем, что нижняя подушка расположена на цилиндрических катках. Условно эту опору изображают в виде двух опорных стержней, нижние шарниры которых расположены на прямой ЬЬ параллельной оси Х (рис. 1.8.3,6, справа). Такая опора может перемещаться перпендикулярно плоскости чертежа. Реакция R действует в плоскости ZХ.

Опора третьего типа—подвижная шаровая опора (рис. 1.8.3, в). Нижняя подушка опоры покоится на шаровых катках. Реакция опоры имеет единственное направление, нормальное к плоскости качения Х Y.

Опора четвертого типа—полное защемление (рис. 1.8.3,г), в которой возникают три составляющие сил Z, Y и Х и три момента.

Опорные реакции для пространственной статически определимой системы находят используя шесть условий равновесия:

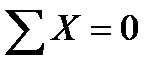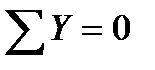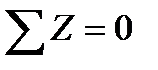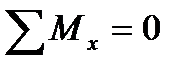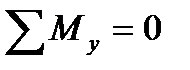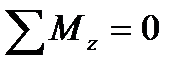, , , , , (1.8.1)

Обычно стремятся оси, относительно которых берутся моменты, выбирать так, чтобы уравнения равновесия содержали наименьшее число неизвестных.

Аналитический признак неизменяемости выражается так:

s=3k , (1.8.2)

где s – число стержней;

k – число узлов.

Пространственная ферма, для которой соблюдается соотношение (1.8.2), может быть неизменяемой. Если s<3k система безусловно изменяема. Если s>3k система имеет лишние связи. Так как условие неизменяемости (1.8.2) является необходимым , но недостаточным, то для окончательного заключения о неизменяемости необходимо провести соответствующий анализ структуры системы или дать аналитическое исследование определенности усилий при действии произвольной нагрузки.

Основные геометрические признаки неизменяемости пространственных ферм:

1) ферма неизменяема, если каждый узел фермы последовательно прикрепляется к трем предыдущим узлам тремя стержнями, не лежащими в одной плоскости;

2) ферма неизменяема, если она составлена из блоков (неизменяемое тело), связанных между собой попарно шестью стержнями расположение которых удовлетворяет условиям неподвижности соединений блоков.

Вообще если имеем п блоков, то число связующих стержней С определяется по формуле:

С=6(п-1) (1.8.3)