Измерение пространственных и временных величин

(времени, площади, объема, скорости, ускорения, плоского угла, телесного угла, длины, например, линейных размеров между поверхностями и осями, размеров и расположения поверхностей, формы поверхности.

Измерение периодических величин -частоты, периода, амплитуды, мощности, энергии)

Язык математических формул, обеспечивает замечательную простоту и компактность описания, необходимую для правильного изложения физических законов и их следствий. Поэтому, вполне правомерно сказать «математика – это язык физики». Но этот язык имеет особые правила и если следовать им, то можно будет извлекать из анализа физических законов абсолютно правильные выводы, например: квадратный корень из 2 равен 1,414... или sin2α =2·sinα·соsα. Но, вместе с тем, необходимо строго следить за тем, чтобы не смешивать такие истины с точными утверждениями относительно самого физического мира.

Геометрические измерения имеют для физики пространства и времени принципиальное значение. Но прежде мы должны решить вопрос - применять евклидову или какую-либо другую геометрию для описания окружающего нас мира? А это, безусловно, является вопросом о физических свойствах Вселенной, то есть, можем ли мы в физических измерениях предполагать, что всегда справедливы аксиомы и теоремы Евклида? Или, не вдаваясь в сложные математические вычисления, мы можем высказать только несколько простых истин об экспериментально определимых, на основании аксиом и теорем Евклида, свойствах пространства. Сложный вопрос, поскольку даже утвердительный ответ на вопрос о том, что измеренное отношение длины окружности к диаметру физического круга действительно равняется 3,14159..., является скорее вопросом эксперимента, а не математического умозаключения.

Геометрия и физика пространства и времени

Одной из наиболее известных теорем математики является теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов прилегающих к ней сторон (катетов) (рис. 1.7). Выполняется ли эта математическая истина также в реальном мире, изучаемом физикой? И может ли быть иначе? Одного умозаключения тут недостаточно, и для ответа мы должны обратиться к опыту.

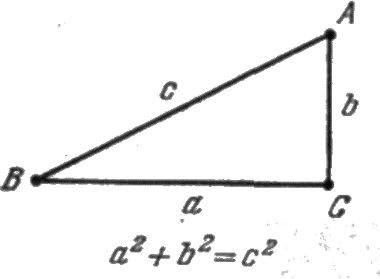
Рис. 1.7. Точно ли описывают физический мир аксиомы Евклидовой геометрии,

из которых логически выводится теорема Пифагора? Это может решить только опыт.

Приведем здесь некоторые соображения, отметив, что они имеют несколько неполный характер, так как мы пока не можем пользоваться метрикой трехмерного пространства, обладающего кривизной.

Вначале вообразим, в каком положении находились бы двумерные разумные существа, живущие в такой Вселенной, которая представляет собой поверхность шара. Математики «двумерного пространства» могли бы дать этим разумным существам описание свойств и других пространств, с тремя и даже большим числом измерений, но им так же трудно было бы представить в своем воображении такие вещи, как и нам — нарисовать себе четырёхмерное пространство.

Как же эти двумерные разумные существа могут установить, что живут на поверхности, обладающей кривизной? Чтобы убедиться в этом, им нужно проверить, что для данной поверхности теряют силу хотя бы некоторые аксиомы геометрии на плоскости, а для этого надо экспериментально установить, выполняются ли определенные теоремы евклидовой геометрии на той поверхности, на которой они живут.

Эти двумерные разумные существа будут проводить «прямые» линии как линии кратчайших расстояний между любыми двумя точками В и С на поверхности шара (рис. 1.8).

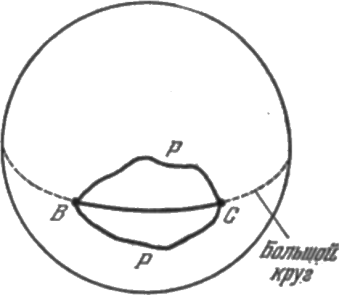
Рис. 1.8. Кратчайшее «прямолинейное» расстояние между точками В и С на шаровой

поверхности проходит по дуге большого круга, соединяющей эти точки,

а не по какому-либо другому пути Р.

Мы считали бы такую линию дугой большого круга. Они могут строить прямоугольные треугольники и проверять на них, выполняется ли теорема Пифагора. Для очень маленького треугольника, каждая из сторон которого мала по сравнению с радиусом шара, теорема будет выполняться с большой, но не с абсолютной точностью. Для большого треугольника обнаружится значительное отклонение от этой теоремы.

Если В и С — точки на экваторе шара, то «прямая» линия, соединяющая их, является дугой ВС экватора (рис. 1.9). Кратчайшим путем из точки С на экваторе к северному полюсу А является линия постоянной долготы (меридиан), пересекающая экватор ВС под прямым углом.

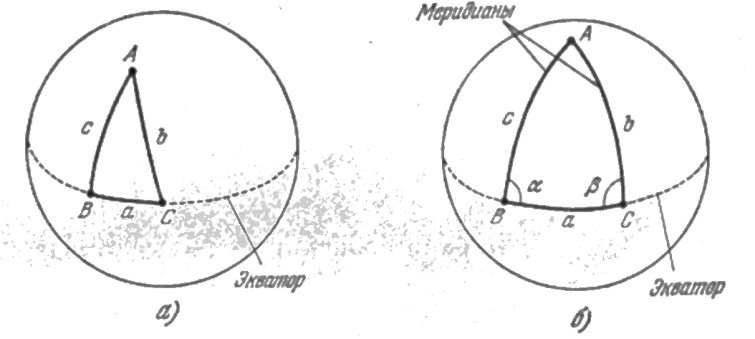
Рис. 1.9. Двумерные существа могли бы строить треугольники с заданными вершинами

А, В, С к отрезками «прямых» линий в качестве сторон. Они нашли бы, что для

маленьких прямоугольных треугольников а² + в² ≈ с² и сумма углов треугольника

немного больше 180° (а). Если бы они рассматривали большие треугольники, то сумма

углов все более превышала бы 180° (б). Здесь точки В и С находятся на экваторе, а точка

А — полюс шара, причем оба угла α и β прямые. Очевидно, что а² + в² ≠ с²,

потому что в=с.

Кратчайшим путем из А в В является отрезок другого меридиана, который также пересекает экватор ВС под прямым углом. Получается прямоугольный треугольник, в котором в=с. Очевидно, что на поверхности шара теорема Пифагора не выполняется, потому что с² не может быть здесь равно а² + в²; далее, сумма внутренних углов треугольника АВС всегда больше 180°. Измерения, сделанные на искривленной поверхности ее двумерными обитателями, дают им возможность убедиться, что эта поверхность действительно обладает кривизной.

Однако эти обитатели всегда могут сказать, что законы геометрии на плоскости точно описывают их двумерный мир, а причина указанного несоответствия связана со свойствами линеек, применяемых для измерения кратчайшего расстояния и определения «прямой» линии. Они могут показать, что метровые линейки не имеют постоянной длины, а растягиваются и сжимаются, когда их переносят в различные места поверхности. Только в результате непрерывных измерений, выполненных различными способами и давших одинаковый результат, становится очевидно, что наиболее простое объяснение нарушения евклидовой геометрии заключается в том, что поверхность имеет кривизну. Аксиомы геометрии на плоскости не являются в этом искривленном двумерном мире самоочевидными истинами; они воо6ще уже не являются истинами. Мы видим, что вопрос о том, какова истинная геометрия Вселенной, представляет собой физическую проблему, подлежащую экспериментальному исследованию. Описывая измерения, выполненные в нашем собственном трехмерном мире, мы обычно не задаем себе вопроса о том, справедлива ли евклидова геометрия, потому что евклидова геометрия является настолько, хорошим приближением к геометрии Вселенной, что при практических измерениях не обнаруживаются какие-либо отклонения от нее. Это не означает, что применимость евклидовой геометрии самоочевидна или что эта геометрия совершенно точно выполняется в мировом пространстве. Великий математик XIX в. Карл Фридрих Гаусс высказал предположение, что необходимо проверить отсутствие кривизны трехмерного пространства, следующее из геометрии Евклида, измеряя сумму внутренних углов большого треугольника (рис. 1.10); он понимал, что если трехмерное пространство обладает кривизной, то сумма углов достаточно большого треугольника должна заметно отличаться от 180°.

Гаусс использовал (1821—1823) геодезические приборы .для точного измерения треугольника, образованного вершинами гор Брокен, Хохехаген и Инзельберг в Германия.

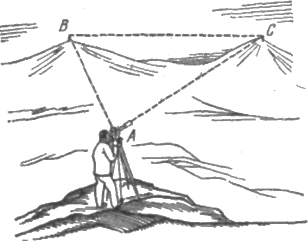
Рис. 1.10. Гаусс измерял углы треугольника, вершины которого находились

на вершинах трех гор, и в пределах точности своих измерений не обнаружил

отклонения суммы углов от 180°

Наибольшая сторона треугольника имела длину около 100 км. Измеренные внутренние углы были равны:

86° 13' 58,366^’’

53° 6' 45,642^’’

40° 39' 30,165^’’

Сумма 180° 00' 14,173^’’

В работах Гаусса нет данных по поводу оценки точности этих значений; вероятно, последние два десятичных знака не являются достоверными. Поскольку на каждой из трех вершин геодезические приборы устанавливались по местной плоскости горизонта, эти три горизонтальные плоскости не были параллельными. Вычисленную поправку, названную сферическим избытком и равную 14,853 дуговой секунды, надо вычесть из полученной суммы углов. Исправленная сумма, равная 179^o59',320^’’, отличается от 180° на 0,680 дуговой секунды. Гаусс считал, что эта величина находится в пределах ошибок измерений, и сделал вывод, что в пределах точности этих измерений пространство является евклидовым.

Из приведенного выше, примера очевидно, что евклидова геометрия дает правильное описание свойств маленького треугольника на обыкновенной двумерной сферической поверхности, а отклонения от евклидовой геометрии становятся все более значительными по мере увеличения размеров. Для того чтобы убедиться, что наше трехмерное физическое пространство действительно является плоским, нам надо произвести измерения с очень большими треугольниками, вершины которых образованы Землей и удаленными звездами или даже галактиками. Однако мы сталкиваемся с такой трудностью: наше положение определяется положением Земли, и мы еще не имеем возможности передвигаться в космическом пространстве с масштабными линейками, чтобы измерять стороны и углы астрономических треугольников.

Измерение длины, площади, плоского угла, телесного угла, объема

При измерении длины тела в каком-либо направлении определяется число, показывающее, сколько раз в этом направлении в теле укладывается выбранный эталон (за эталон принимается некоторый твердый стержень, а его длина - за единицу длины). Это число и называется длиной тела в рассматриваемом направлении. Если оно не целое, то предварительно длину эталона следует разделить на более мелкие части: десятые, сотые и пр. Используя их наряду с самим эталоном, можно представить длину всякого тела в виде десятичной дроби или целого числа с десятичной дробью.

Измерение длины непосредственным прикладыванием эталона или его частей и называется прямым измерением. Прямые измерения длины не всегда возможны, они невозможны, например, при измерении расстояний до удаленных тел, например планет, звезд и других небесных объектов. Они невозможны и при измерении очень малых длин, например таких, с которыми имеет дело физика атома, атомного ядра или элементарных частиц. Во всех этих случаях применяют косвенные методы. Правильность таких методов должна контролироваться прямыми методами (разумеется, в тех случаях, когда они применимы).

То есть, косвенные методы остаются за пределами применимости прямых методов. Прямые измерительные операции, с помощью которых первоначально было введено количественное понятие длины, становятся в этом случае чисто умозрительными, а косвенные методы играют роль измерительных операций, раскрывающих смысл измеряемой длины, или, точнее, тех чисел, которыми длины характеризуются.

Примером косвенного метода измерения длины может служить триангуляция, применяемая для измерения расстояний до удаленных предметов. А именно, прямым методом измеряют длину «базы» АВ (основание треугольника АВС), с концов которой делают «засечки» удаленного объекта С, т. е. измеряют углы между базой АВ и прямыми АС и ВС. По этим данным искомое расстояние до объекта С может быть найдено геометрическим построением или вычислено по формулам геометрии. Если база АВ настолько велика, что ее длина не может быть найдена прямым измерением, то можно выбрать более короткую базу и затем найти длину базы АВ описанным косвенным методом.

Измерение времени

Что есть «время»???.

Как и всякая физическая величина, время количественно характеризуется некоторыми числами. Важно выяснить, с помощью каких принципиальных измерительных операций эти числа могут быть получены и, тем самым, будет установлен точный смысл самих этих чисел.

Обычно под временем в количественном смысле этого слова понимают показания каких-то часов. То есть, говорят не о самом времени, а о промежутке времени между двумя последовательными событиями или моментами времени. Он характеризуется разностью показаний часов в рассматриваемые моменты времени. Даже когда говорят просто о времени, не указывая оба момента, являющиеся границами рассматриваемого промежутка времени, то предполагают, что один из этих моментов фиксирован и условно считается начальным. От него и ведется отсчет времени.

Часы здесь должны пониматься в широком смысле слова, как некоторое тело или систему тел, в которых совершается периодический процесс, служащий для измерения времени. Примерами таких процессов могут и служить колебание маятника с постоянной амплитудой, и вращение Земли вокруг собственной оси относительно Солнца или звезд, и колебания атома в кристаллической решетке, и колебания электромагнитного поля, представляемого достаточно узкой спектральной линией, и пр.

Так, если между какими-либо двумя событиями Земля при вращении относительно звезд сделала один оборот, то говорят, что промежуток времени между этими двумя событиями составляет звездные сутки. Если при этом она совершила 10 оборотов, то соответствующий промежуток времени будет 10 звездных суток, и т.д. Если в течение звездных суток маятник совершил приблизительно 86 164 колебания, то говорят, что период одного колебания составляет одну секунду, и т.д. От звездных суток следует отличать солнечные сутки. Так называется промежуток времени, в течение которого Земля делает один оборот при вращении вокруг собственной оси относительно Солнца. Ввиду того, что Земля движется вокруг Солнца не по круговой, а по эллиптической орбите, это ее движение не совсем равномерно. Это значит, что солнечные сутки изо дня в день несколько изменяются в течение года. Поэтому при измерении времени пользуются, так называемыми, средними солнечными сутками. Они составляют 24 часа = 24×60 = 1440 минут = 1440×60 = 86 400 секунд.

К часам предъявляют требования, чтобы они шли «равномерно». Но что значит, что часы идут равномерно? Говорят, это означает, что периодический процесс, служащий для отсчета времени, должен повторяться через строго одинаковые промежутки времени. Однако убедиться в одинаковости следующих друг за другом промежутков времени можно только в том случае, когда мы уже располагаем равномерно идущими часами. Выйти из этого порочного логического круга можно только путем определения, так как никакого априорного представления о равномерном течении времени не существует, поэтому надо условиться считать какие-то часы по определению равномерно идущими. Такие часы должны рассматриваться как эталонные или основные часы, по которым должны градуироваться все остальные.

В принципе любые часы могут быть приняты как эталонные. Однако так поступать не целесообразно. Эталонные часы должны быть достаточно «хорошими», то есть, прежде всего, обладать высокой воспроизводимостью. Это означает, что если изготовить с возможной тщательностью много «одинаковых» эталонных часов, то они с большой точностью должны идти одинаково, независимо от того, изготовлены ли они одновременно, или между моментами их изготовления прошло длительное время. Например, песочные часы дают несравненно худшую воспроизводимость, чем маятниковые часы. Наилучшая воспроизводимость была достигнута только после изобретения кварцевых, молекулярных и атомных часов.

Наконец, за единицу времени могут быть приняты либо средний тропический год, либо некоторая доля его. Для того чтобы разделить эталон времени — средний тропический год — на равные чести, применяются те или иные часы. Чаще всего часы - это устройство, в котором происходит какой-либо периодический процесс (т. е. процесс, повторяющийся через равные промежутки времени). Сосчитав число периодов процесса, происходящих в часах в течение среднего тропического года, мы можем разделить год на известное число равных частей и пользоваться продолжительностью одного периода, т. е. известной долей среднего тропического года, как единицей времени. За единицу времени в физике принята 1 секунда, составляющая определенную с высокой точностью долю среднего тропического года.

Часы представляют собой, таким, образом, физический прибор, служащий при измерении времени той же цели, какой служит линейка с нанесенными на ней делениями (расстояние между которыми составляет известную долю эталона длины) при измерении длины. Как и всякий физический измерительный прибор, часы должны удовлетворять известным требованиям, и прежде всего происходящий, в них процесс должен быть точно повторяющимся.

Для разделения эталона времени — среднего тропического года — на равные части, кроме часов с маятником, сейчас применяют, другие типы часов, например кварцевые часы, в которых периодическим процессом служат упругие колебания пластинки, вырезанной из пьезоэлектрического кристалла кварца (эти колебания поддерживаются при помощи схемы с электронными лампами). В последнее время были созданы молекулярные и атомные часы, в которых используются периодические колебания, происходящие в атомах или молекулах; чтобы число этих колебаний можно было считать (с помощью специальных электрических устройств), выбирают такие колебания которым соответствуют спектральные линии, лежащие в области радиоволн.